謝爾品斯基猜想

謝爾品斯基猜想（Sierpiski conjecture）是關於單位分數的著名猜想。該猜想可表述為：當n較大時，真分數m/n 能表示成三個單位分數(不一定相異)的和。

基本介紹

• 中文名：謝爾品斯基猜想
• 外文名：Sierpiski conjecture 
• 性質：關於單位分數的著名猜想
• 特點：未證明是否成立
• 重要套用：歐拉函式的取值
• 學科：數學

謝爾品斯基猜想

謝爾品斯基猜想（Sierpiski conjecture）是關於單位分數的著名猜想。該猜想可表述為：當 為正整數， ，且 較大時，不定方程

一定有正整數解。

古埃及的蘭德紙草書上就記載了用單位分數 表示真分數的方法。後來知道任何真分數 都能表為兩個或三個相異的單位分數的和：

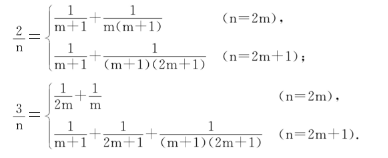
1950年，愛爾特希(Erdo¨s，P.)猜想 能表示成三個相異的單位分數的和。

謝爾品斯基(Sierpiski，W.)猜想 也能表示成三個單位分數的和。

謝爾品斯基還進一步猜想：在 較大時，真分數 都能表示成三個單位分數(不一定相異)的和，即上述不定方程有正整數解。這裡要限定 較大，是因為 較小時發現有猜想不成立的例子。比如已證明 至少需要4個單位分數的和才能表示它。至今還未能證明上述猜想是否成立。

有關歐拉函式的謝爾品斯基猜想

所謂歐拉函式 指的是，在 中與 互素的整數的個數。有關歐拉函式取值的謝爾品斯基猜想表述如下：

設 為一給定的正整數，它可以作為 值出現的次數，即滿足 的不同的正整數 的個數，稱為整數 的重數。

例如，6的重數是4，這是因為若且唯若 時， 成立。由於對於 均為偶數，故對於所有大於1的奇數 ，它們的重數都是0。重數為0的偶數有

等。它們都是使方程 沒有整數解 的 。在小於 範圍內，這樣的偶數有26663個。