y 是 J 的內平穩函式,每個內平穩函式滿足方程,則這個方程稱為諾特方程。
基本介紹
- 中文名:諾特方程
- 外文名:Noether equation
- 適用範圍:數理科學
簡介,內變分,定義,性質,推論,
簡介
內變分
內變分是變分積分相對於未知函式的自變數的變化的變化率。
對一維情形,設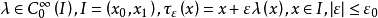 (ε0是適當小的正數)使
(ε0是適當小的正數)使 ,令
,令 ,若 y 是泛函
,若 y 是泛函
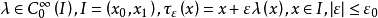



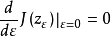

定義
若一個函式 y 使對任意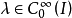 有
有 ,則稱 y 是 J 的內平穩函式,每個內平穩函式
,則稱 y 是 J 的內平穩函式,每個內平穩函式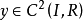 滿足方程
滿足方程
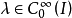

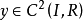

性質
對一般的變分積分





推論
由



y 是 J 的內平穩函式,每個內平穩函式滿足方程,則這個方程稱為諾特方程。
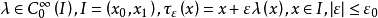



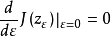

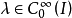

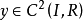









y是 J 的內平穩函式,每個內平穩函式滿足方程,則這個方程稱為諾特方程。...... y是 J 的內平穩函式,每個內平穩函式滿足方程,則這個方程稱為諾特方程。...
諾特定理,是奇異積分方程的基本定理,為理論物理的中心結果之一,它表達了連續對稱性和守恆定律的一一對應。諾特定理對於所有基於作用量原理的物理定律是成立。它得名...
特普利茨方程是一類理論上重要的奇異積分方程.設已給函式a(t)EL00,t定義在單位圓周上。...
在物理學裡,連續性方程(英語:continuity equation)乃是描述守恆量傳輸行為的偏微分方程。由於在各自適當條件下,質量、能量、動量、電荷等等,都是守恆量,很多種傳輸...
它早期的著名例子是輻射傳輸理論中的米爾恩方程,後來因1931年N.維納和E.霍普夫給出其求解方法而得名。20世紀40年代以後,這一方程的理論在解析函式邊值問題、調和...
