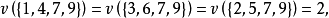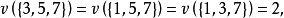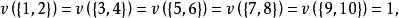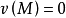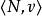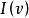諾伊曼-莫根施特恩解(Neumann-Morgenstern solution)亦稱穩定集,是合作對策的基本概念之一,指合作對策分成集的某個子集。馮·諾伊曼(J.von Neumann)和莫根施特恩(O.Morgenstern)曾經提出把滿足所謂內部穩定性和外部穩定性的一組分成作為合作對策的解,但這樣的解對於本質合作對策並不惟一,甚至還比對策核中的元素多,內部穩定性指集合R中的分成不優於集內其他分成,外部穩定性指對集合R以外的任意分成x,存在R內的分成y優於x,若一個合作對策具有核C和諾伊曼-莫根施特恩解R,則C是R的子集,若一個合作對策的諾伊曼-莫根施特恩解R僅由惟一的一個分成x構成,則此對策的特徵函式V是非本質的。任何非本質合作對策的諾伊曼-莫根施特恩解為:x=(V(1),V(2),…,V(n)),但對於具有兩個或兩個以上局中人的本質合作對策,諾伊曼-莫根施特恩解一般不止一個。
基本介紹
- 中文名:諾伊曼-莫根施特恩解
- 外文名:Neumann-Morgenstern solution
- 所屬學科:數學
- 別名:穩定集、N-M解
- 所屬問題:運籌學(對策論)
定義,定理,例題解析,
定義
馮·諾伊曼和摩根斯坦恩在1944年提出了穩定集這個解概念。
(1) 如果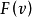 中的任何兩個分配都沒有優超關係(即不存在一個分配通過一個聯盟占優另一個分配),則稱
中的任何兩個分配都沒有優超關係(即不存在一個分配通過一個聯盟占優另一個分配),則稱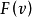 是內部穩定的。
是內部穩定的。
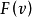
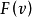
(2) 如果任取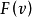 外的一個分配
外的一個分配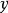 ,存在分配
,存在分配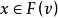 ,使得
,使得 優超
優超 ,則稱
,則稱 是外部穩定的。既是內部穩定的,又是外部穩定的分配集稱為穩定集(也稱為N-M解,諾伊曼-莫根施特恩解)。
是外部穩定的。既是內部穩定的,又是外部穩定的分配集稱為穩定集(也稱為N-M解,諾伊曼-莫根施特恩解)。
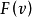
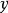
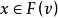



定理
定理 核心必定屬於穩定集,但穩定集不一定是核心。
核心裡的任一個分配都不被其他分配優超,所以核心一定滿足內部穩定,如果核心中有一個分配 不屬於穩定集,則穩定集裡一定存在一個分配
不屬於穩定集,則穩定集裡一定存在一個分配 優超分配
優超分配 ,這與核心中的任一分配不被優超矛盾,所以核心屬於穩定集。
,這與核心中的任一分配不被優超矛盾,所以核心屬於穩定集。



例題解析
有一家商店在搞打折促銷的活動,優惠的方法是:單買一件棉衣100元;如果一次購買2件棉衣,第二件半價,即只要150元,但沒有其他形式的優惠.現恰有互不相識的甲、乙、丙3人在店裡都想買一件棉衣,則他們如果兩個人合作,兩人總共可以少花50元,如果3個人合作,也只可以節省50元,討論該問題的穩定集。
解: 這個博弈的特徵函式可以寫為


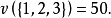
一個博弈可能形成哪一個聯盟,這要考慮這個博弈所面對的現實環境的多種因素,如本題這個簡單的例子,對於兩人聯盟,聯盟外的第三個局中人會設法(如給聯盟中一個局中人更高的收益)使一個局中人脫離原聯盟與自己組成聯盟。而三個人的聯盟與兩個人的聯盟的收益一樣多,三個人結成的大聯盟更有問題,前面已經假設一個聯盟形成後,在整個博弈過程中不變,因此形成了三人大聯盟,就假設三人大聯盟在分析時不破裂,注意這是決策的分析,不是現實中的實施,分析要全面,只有分析全面了,現實中的實施才更有保障。
這個博弈例子沒有核心。
分配集的一個子集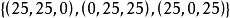 就是這個博弈的一個穩定集
就是這個博弈的一個穩定集 。因為這個集合中的任兩個分配之間不存在優超關係。對集合外的一分配,例如
。因為這個集合中的任兩個分配之間不存在優超關係。對集合外的一分配,例如 ,這裡
,這裡 。分配
。分配 中關於聯盟
中關於聯盟 優超分配
優超分配 。
。
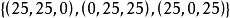






現對穩定集 外的任一分配
外的任一分配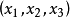 。因為是分配,所以
。因為是分配,所以 ,假設穩定集中的三個分配都不優超分配
,假設穩定集中的三個分配都不優超分配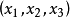 。
。

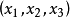

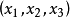
分配 不優超分配
不優超分配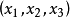 ,所以
,所以 或者
或者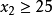 ;
;

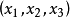

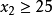
分配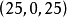 不優超分配
不優超分配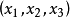 ,所以
,所以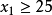 或者
或者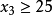 ;
;
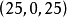
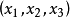
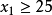
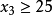
分配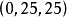 不優超分配
不優超分配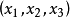 ,所以
,所以 或者
或者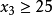 ;
;
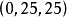
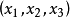

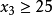
因此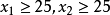 或者
或者 至少有兩個必須同時成立,設是
至少有兩個必須同時成立,設是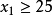 和
和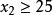 ,又因為
,又因為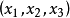 是一個分配,所以
是一個分配,所以 ,要這些都成立,只有
,要這些都成立,只有 ,且
,且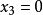 。這是穩定集中的一個分配,與
。這是穩定集中的一個分配,與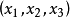 是穩定集外的分配矛盾,因此假設錯誤,則集合
是穩定集外的分配矛盾,因此假設錯誤,則集合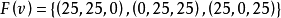 外的任一分配都至少被該集合內的一個分配優超。
外的任一分配都至少被該集合內的一個分配優超。
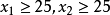

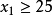
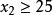
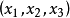


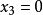
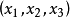
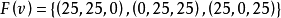
核心是一個唯一確定的集合,但穩定集不是,一個博弈可以有多個穩定集,並且穩定集也有可能是空集,盧卡斯(lucas)在1968年舉出下面這個沒有穩定集的合作博弈:
博弈 ,其中
,其中 ,有特徵函式:
,有特徵函式: