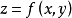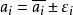誤差分析

誤差分析是指對誤差在完成系統功能時，對所要求的目標的偏離產生的原因、後果及發生在系統的哪一個階段進行分析，把誤差減少到最低限度。

研究誤差的目的，不是要消除它，因為這是不可能的；也不是使它小到不能再小，這不一定必要，因為這要花費大量的人力和物力；而是在一定的條件下得到更接進於真實值的最佳測量結果。

基本介紹

• 中文名：誤差分析
• 外文名：Error analysis
• 學科：數學
• 本質：對不確定性的種類和數量的研究
• 目的：降低誤差
• 相關名詞：相對誤差

基本信息

在數學中，誤差分析是對解決問題可能存在的錯誤或不確定性的種類和數量的研究。 這個問題在數值分析和統計等套用領域尤為突出。

誤差分析

在實際系統的數值模擬或建模中，隨著模型參數的變化，誤差分析與模型輸出的變化有關。

例如，在作為兩個變數的函式建模的系統中。 誤差分析涉及x和y（在平均值和附近）的數值誤差以及z（在平均值附近）的數值誤差。

在數值分析中，誤差分析包括前向誤差分析和後向誤差分析。

前向誤差分析

前向誤差分析涉及函式的分析，它是函式確定近似誤差的界限（通常是有限多項式）；舉個例子，找到一個，使得。

後向誤差分析

後向誤差分析涉及近似函式，以確定參數，使結果。

後向誤差分析，其理論由詹姆斯·威爾金森（James H. Wilkinson）提出和推廣，可用於確定實現數字函式的算法在數值是否穩定。方法表明，儘管由於捨入誤差而導致的計算結果不完全正確，但這是一個精確的解決方案。 如果所需的擾動小，按照輸入數據的不確定性的順序，則結果在某種意義上與數據“應得的”一樣準確。 然後將算法定義為向後穩定。 穩定性是對給定數值程式的捨入誤差敏感度的量度;；相比之下，給定問題的函式的條件數表示函式對其輸入中的小擾動的固有靈敏度，並且獨立於用於解決問題的實現。

套用

全球定位系統

使用全球定位系統計算的誤差分析對於了解GPS的工作原理以及了解應該預期的幅度誤差很重要。 全球定位系統對接收機時鐘誤差和其他影響進行修正，但仍然存在未糾正的殘差錯誤。 全球定位系統（GPS）由美國國防部（DOD）於七十年代創建。 它已經被美軍和公眾廣泛地用於導航。

分子動力學模擬

在分子動力學（MD）模擬中，由於相空間或不經常發生的事件的採樣不足，存在誤差，這導致了測量中隨機波動引起的統計誤差。

對於波動特性A的一系列M測量，平均值為：

當這些測量是獨立的時候，平均值<A>的方差是：

其中是自相關函式，由

然後我們可以使用自動相關函式來估計誤差。

科學數據驗證

測量通常具有少量的誤差，同一項目的重複測量通常會導致讀數略有不同。 可以分析這些差異，並遵循一定的已知數學和統計特性。一般來說，誤差分析通常不足以證明數據被偽造或製造，但它可能提供必要的支持證據，以證實懷疑不當行為。

相關內容

物理化學以測量物理量為基本內容，並對所測得數據加以合理的處理，得出某些重要的規律，從而研究體系的物理化學性質與化學反應間的關係。

然而，在物理量的實際測量中，無論是直接測量的量，還是間接測量的量（由直接測量的量通過公式計算而得出的量），由於測量儀器、方法以及外界條件的影響等因素的限制，使得測量值與真實值（或實驗平均值）之間存在著一個差值，這稱之為測量誤差。

研究誤差的目的是：在一定的條件下得到更接進於真實值的最佳測量結果；確定結果的不確定程度；據預先所需結果，選擇合理的實驗儀器、實驗條件和方法，以降低成本和縮短實驗時間。因此我們除了認真仔細地做實驗外，還要有正確表達實驗結果的能力，這二者是同等重要的。僅報告結果，而不同時指出結果的不確定程度的實驗是無價值的，所以我們要有正確的誤差概念。