基本介紹
- 中文名:設定誤差
- 外文名:specification error
- 所屬學科:數學(統計學)
- 所屬問題:經濟計量學方法(經濟計量模型)
- 別稱:設定偏誤
設定誤差的含義




設定誤差的類型
漏掉一個有關變數






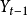
包含一個無關變數
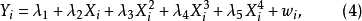




採用錯誤的函式形式

測量誤差




對隨機誤差項設定不正確
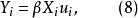


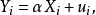















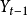
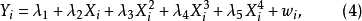









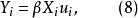


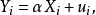




設定誤差(specification error)亦稱“設定偏誤”,指由經濟計量模型設定條件的錯誤,引起的未知參數最小二乘估計的誤差。模型設定條件的錯誤主要有:1)遺漏了重要的解釋...
誤差線是通常用於統計或科學數據,顯示潛在的誤差或相對於系列中每個數據標誌的不確定程度。誤差線可以用標準差(平均偏差)或標準誤差,一般通用的是這兩個,如果是發...
在測量時,測量結果與實際值之間的差值叫誤差。真實值或稱真值是客觀存在的,是在一定時間及空間條件下體現事物的真實數值,但很難確切表達。測得值是測量所得的...
《誤差與數據處理》是2008年化學工業出版社出版的圖書,作者是毛丹弘。本書適合中等職業學校化學化工類以及相關專業學生使用,也可作為從事化學化工教學的教師及相關行...
平均絕對誤差(Mean Absolute Deviation),又叫平均絕對離差,是所有單個觀測值與算術平均值的偏差的絕對值的平均。平均絕對誤差可以避免誤差相互抵消的問題,因而可以準確...
調查誤差(Error in Survey)是指在取得樣本數據資料過程中產生的誤差。這部分誤差通常與調查者、回答者、資料蒐集方式和問卷等因素有關,它們會形成在調查過程中出現...
回程誤差是指在相同條件下,被測量值不變,計量器具行程方向不同其示值之差的絕對值。也稱滯後誤差。測量器具對同一個尺寸進行正向和反向測量時,由於結構上的原因,...
視準軸誤差是指視準軸與水平軸的不正交誤差,在望遠鏡的安裝過程中容易出現這種誤差,視準軸誤差主要影響水平方向觀測值。簡稱2C。...
誤差與遺漏是指編制國際收支平衡表時,因資料不完整、統計時間和計價標準不一致以及貨幣換算等因素所造成的差錯和遺漏,它是為使國際收支核算保持平衡而設定的平衡項目...
穩態誤差係數(Steady State Error Coefficient),即靜態誤差係數,是為了方便反映控制系統穩態誤差而設定的係數。對不同的輸入量加以區分,主要有靜態位置誤差係數、靜態...
點位中誤差表示點位精度的一種數值指標,屬於函式的中誤差,依各坐標分量中誤差通過計算求得。在X軸和Y軸方向的誤差的平方和的平方根。它屬於函式的中誤差。直接...
②選擇較好的接收機天線,在天線中設定徑板,抑制極化特性不同的反射信號GPS誤差與GPS 接收機有關的誤差 編輯 (1)接收機鐘差GPS 接收機一般採用高精度的石英鐘,...
6.輸入標準變比後,能自動計算出相對誤差。7. 一次測量完成,自動切斷試驗電壓 。8. 設定數據,測量結果自動保存,可查看以前數據。9. 測量有載變壓器,只輸入一次...
誤差理論與測量平差基礎,作者是武漢大學測繪學院測量平差學科組 ,由武漢大學出版社出版,是闡述了測量誤差的基本理論,測量平差的基礎方法的一本書。...
有限元誤差模型指的是運用有限元方法對目標物體進行計算的過程中建立的誤差模型。...... 連續體離散為簡單形狀單元體的集合,有限元法中,單元與單元之間的設定的相互...
概念為了保證實驗數據的準確性,每個孔要做一定數量的重複,測量的時候取這幾個孔的平均值。設定復孔的意義1.做細胞試驗的隨機性比較大,設多個復孔可以去除部分...
反映測量結果與真值接近程度的量,稱為精度,它與誤差的大小相對應,因此可用誤差...在結構設計中,應為不同環節設定不同的精度,為敏感環節設定較高精度,這樣可以...
