基本介紹
- 中文名:解耦控制
- 外文名:decoupling control
工程背景
主要分類
相關解法
完全解耦控制
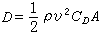
靜態解耦控制
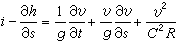

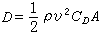
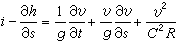
耦合是指兩個或兩個以上的體系或兩種運動形式間通過相互作用而彼此影響以至聯合起來的現象。 解耦就是用數學方法將兩種運動分離開來處理問題,常用解耦方法就是忽略或...
所謂解耦控制,就是採用某種結構,尋找合適的控制規律來消除系統中各控制迴路之間的相互耦合關係,使每一個輸入只控制相應的一個輸出,每一個輸出又只受到一個控制的...
解耦控制問題是線性系統理論上的經典問題,表示選擇適當的控制規律將一個多變數系統化為多個獨立的單變數系統的控制問題。該問題最早在30年代末提出,1969年由E.G....
多變數系統的迴路之間存在著耦合,為了獲得滿意的控制效果,必須對多變數系統實行解耦控制對於絕大多數的多變數系統,將多變數系統解耦為單變數系統來控制是一種較好的...
解耦PID控制即利用PID控制器完成解耦運算的一種方法。在工業過程控制中要求系統能夠安全穩定地運行,有較好的調節性能,能以較小的誤差跟蹤設定值的變化,或使誤差為零...
所謂解耦補償控制(Compensation decoupling control),就是採用某種結構,基於基於不變性原理組成,尋找合適的控制規律來消除系統中各控制迴路之間的相互耦合關係,使每一個...
《多變數自適應解耦控制及套用》是2001年科學出版社出版的圖書,作者是柴天佑。...... 《多變數自適應解耦控制及套用》是2001年科學出版社出版的圖書,作者是柴天佑。...
所謂解耦控制系統,就是採用某種結構,尋找合適的控制規律來消除系統中各控制迴路之間的相互耦合關係,使每一個輸入只控制相應的一個輸出,每一個輸出又只受到一個控制...
聯合控制利用 PR 控制器可無靜差地跟蹤交流參考量 、PI 控制器可無靜差地跟蹤直流參考量的特性 ,提出基於比例諧振(PR)與比例積分(PI)聯合控制的併網逆變器直流...
以保證生產過程的參量為被控制量使之接近給定值或保持在給定範圍內的自動控制系統。這裡“過程”是指在生產裝置或設備中進行的物質和能量的相互作用和轉換過程。表征...
反饋補償解耦控制(Feedback decoupling control)是指將系統的輸出信息返送到輸入端,與輸入信息進行比較,並利用二者的偏差進行控制的,作為被控的輸出以一定方式返回到...
通過控制轉子磁鏈,然後分解定子電流而獲得轉矩和磁場兩個分量,經坐標變換,實現正交或解耦控制。綜合以上:矢量控制無非就四個知識:等效電路、磁鏈方程、轉矩方程、坐標...
多層控制方法,第 1 層為改進的 PQ 下垂算法,對系統的頻率及初始相位同時進行調節,以兼顧提高系統的動態和穩態性能;第 2 層控制檢測系統交流母線電壓的頻率及幅值...
電機控制是指,對電機的啟動、加速、運轉、減速及停止進行的控制。根據不同電機的類型及電機的使用場合有不同的要求及目的。...
最佳化與控制,本書主要介紹了建模技術、軟測量技術、先進控制算法和最佳化算法等理論與技術,這些技術與流程工業有著密切的聯繫。...
《計算機過程控制系統》是2000年由機械工業出版社出版的圖書,作者是劉寶坤。...... 一、均勻控制系統二、比值控制系統第六節 多變數解耦控制系統一、系統的關聯和耦...
非線性系統理論,nonlinear systems theory,是在自動控制理論中研究非線性系統的運動規律和分析方法的一個分支學科。...
