實際構件中的裂紋往往不是單一型的,由於載荷不對稱,結構不對稱,或者裂紋的方位不對稱以及材料各向異性等情況,常使得裂紋尖端附近區域的應力場裡,同時摻雜著型Ⅰ和Ⅱ型甚至Ⅲ型裂紋的應力,這種裂紋稱為複合型(亦稱混合型)裂紋。
基本介紹
- 中文名:複合型裂紋
- 外文名:mixed mode crack
- 同類:單一型裂紋
- 套用學科:力學術語
- 範疇:數理科學
- 涉及:裂紋
概述
基本原理

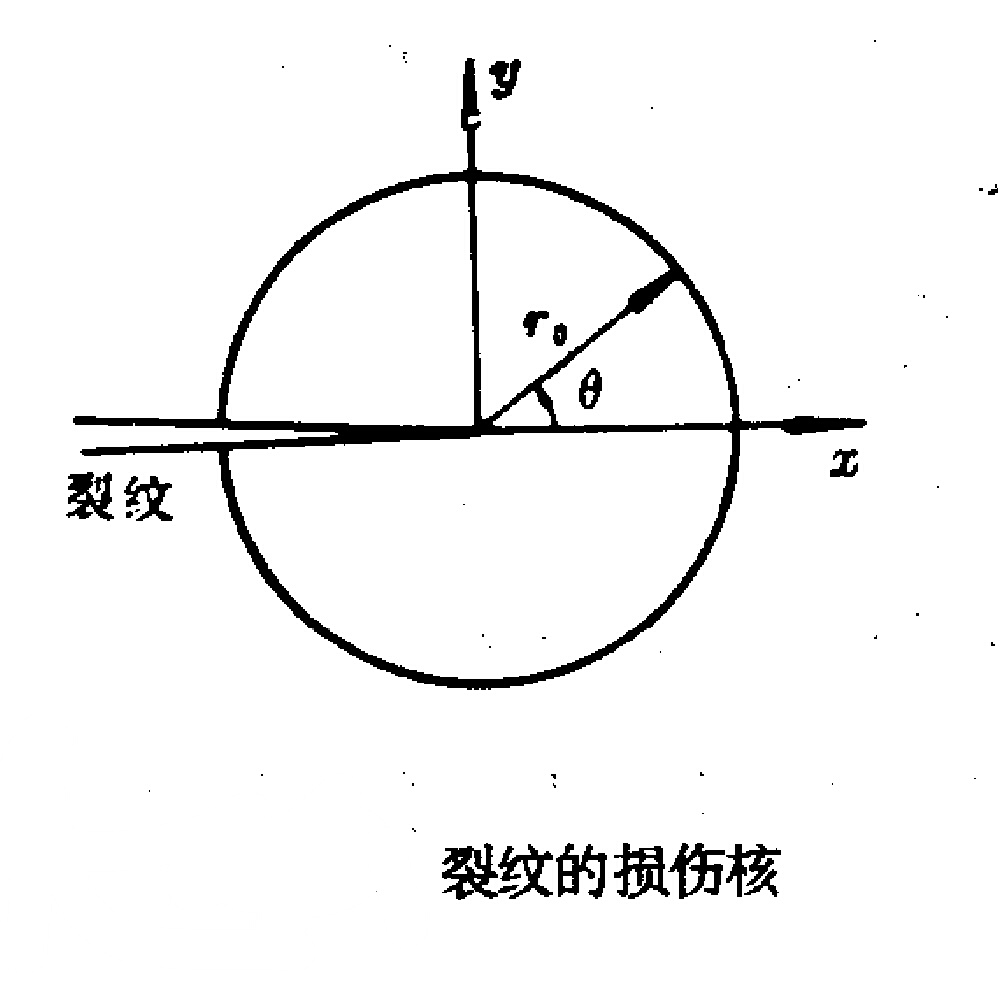 圖1
圖1





























實際構件中的裂紋往往不是單一型的,由於載荷不對稱,結構不對稱,或者裂紋的方位不對稱以及材料各向異性等情況,常使得裂紋尖端附近區域的應力場裡,同時摻雜著型Ⅰ和Ⅱ型甚至Ⅲ型裂紋的應力,這種裂紋稱為複合型(亦稱混合型)裂紋。

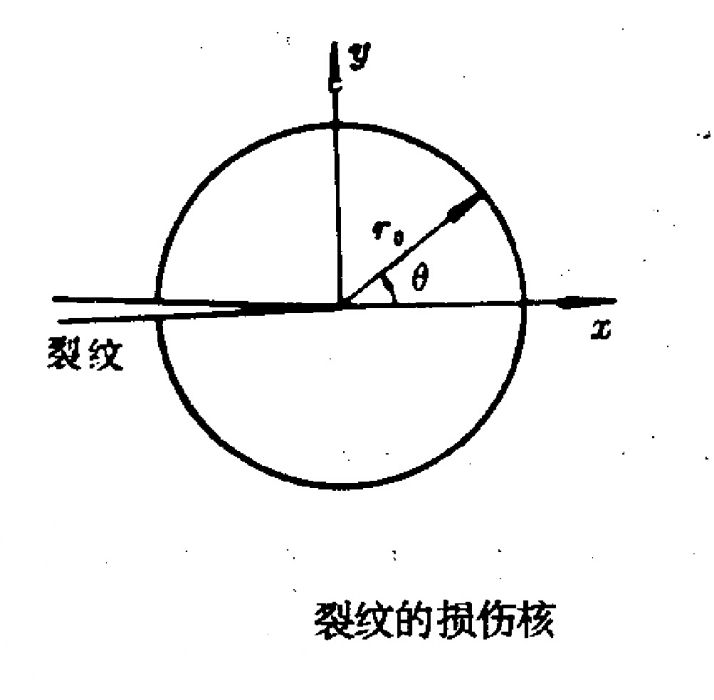
 圖1
圖1





























實際構件中的裂紋往往不是單一型的,由於載荷不對稱,結構不對稱,或者裂紋的方位不對稱以及材料各向異性等情況,常使得裂紋尖端附近區域的應力場裡,同時摻雜著型Ⅰ和...
5.5 複合型裂紋脆斷試驗5.6 理論與實驗比較5.7 塑性變形對金屬材料複合型裂紋脆性斷裂的影響參考文獻第6章 彈塑性斷裂力學6.1 J積分原理...
11.1 複合型裂紋問題萬代 11.2 最大拉應力理論 1l. 3 能量釋放率理論 1l.4 應變能密度理論 11.5 近似斷裂判據 疲勞斷裂篇
採用修正的剪滯理論建立了岩石、混凝土等準脆性材料的I-I I複合型裂縫在單向拉伸荷載作用的計算模型,得到了與實驗相吻合且優於傳統S判據的斷裂角。通過對遠場應力...
第1章介紹斷裂力學的研究對象、研究內容及脆性破壞特徵;第2章介紹雜交位移不連續法的基本理論:第3—8章論述多種含缺陷結構的裂紋問題;第9章論述複合型裂紋的斷裂...
Ⅰ—Ⅲ複合型裂紋的開裂方向和斷裂準則 疲勞損傷演化過程的能量耗散結構研究 循環內塑性應變能及其能耗速率分析模型 材料的循環非彈性回響及其機率分布規律研究 ...
2.6 複合型裂紋的斷裂判據 2.6.1 最大周向應力理論 2.6.2 應變能密度因子理論 2.6.3 最大應變能釋放率理論 2.6.4 複合型斷裂的工程判據 ...
2.5.1 張開型裂紋情況2.5.2 複合型裂紋情況參考文獻第3章 二維應力強度因子邊界配位解法3.1 平面問題極坐標系分離變數解法3.1.1 平面問題極坐標系基本方程...
31. 鄧宗才等. 混凝土複合型裂縫最大拉應變斷裂準則. 華中理工大學學報, 1999, 27(2): 49-51.32. 鄧宗才等. 鋼纖維高強混凝土的斷裂韌度. 工業建築, 1995,...
1.4 裂紋尖端的塑性區及K因子的塑性修正1.4.1 屈服判據1.4.2 裂紋前端屈服區的大小1.4.3 塑性區修正第二章 複合型裂紋2.1 最大周向應力準則...
