補三面角

補三面角(supplementary trihedral angle)亦稱極三面角，是與一個三面角有關的三面角。從三面角S-ABC的頂點S作三條射線SA′，SB′，SC′分別垂直於平面BSC，CSA，ASB，並分別與SA，SB，SC在各相應平面的同側，則三面角S-A′B′C′稱為S-ABC的補三面角，這時S-ABC也是S-A′B′C′的補三面角。一個三面角的每個面角(或二面角)與它的補三面角的對應二面角(或面角)互補。

基本介紹

• 中文名：補三面角
• 外文名：supplementary trihedral angle
• 別名：極三面角
• 所屬學科：數學
• 所屬問題：立體幾何（三面角）
• 簡介：與一個三面角有關的三面角

基本概念

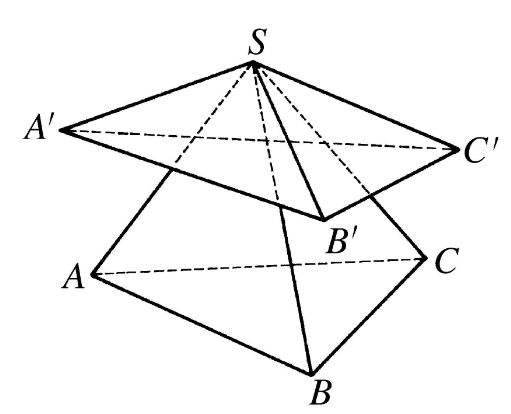
在三面角O-ABC中，在平面BOC的含有棱OA的一側，過O點作射線OA'垂直於平面BOC，類似地作垂直於平面AOC、AOB的垂線OB'、OC'；則以OA'、OB'、OC'為棱的三面角O-A'B'C'叫做三面角O-ABC的補三面角。

圖1

補三面角的性質定理

圖1中，三面角O-A'B'C'是三面角O-ABC的補三面角；同時，三面角O-ABC也是三面角O-A'B'C'的補三面角。於是三面角O-ABC與三面角O-A'B'C'叫做互補三面角。為了證明這個“互補”性質，先證一個引理。

引理 從平面上一點引兩條射線，一條為平面的垂線，一條為平面的斜線。那么這兩條射線形成銳角的充要條件是它們在平面的同側。

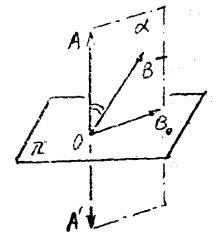圖2

證明設平面π上一點O(圖2)，過O引垂線OA (反向延線OA')，斜線OB，又設射線OB在π上的射影OB₀，則射線OA、OA'、OB、OB₀在同一平面(α)內，並且∠AOB₀=90°，於是有

若射線OA與OB在π的同側，則∠AOB<∠AOB₀，即∠AOB為銳角；

若∠AOB為銳角，則射線OB在∠AOB₀內，即射線OA、OB在平面的同側。

定理1 若三面角O-A'B'C'是三面角O-ABC的補三面角，則三面角O-ABC也是三面角O-A'B'C'的補三面角。

證明 由已知補三面角的定義和引理得：

OB'⊥平面COA，OC'⊥平面AOB，∠AOA'<90°；

因而有：OB'⊥OA，OC'⊥OA，∠AOA< 90°；

即OA⊥平面B'OC'，射線OA與OA'在平面B'OC'的同側。

同理，OB⊥平面C'OA'，射線OB與OB'在平面C'OA'的同側；OC⊥平面A'OB'，射線OC與OC'在平面A'OB'的同側。

∴三面角O-ABC是三面角O-A'B'C'的補三面角。

定理2 兩個互補的三面角中，一個三面角的面角與另一個三面角的相應二面角互補。

證明 在圖3中，三面角O-ABC與三面角O-A'B'C'互為補三面角，先證明面角∠A'OC'與相應的二面角A-OB-C互補。

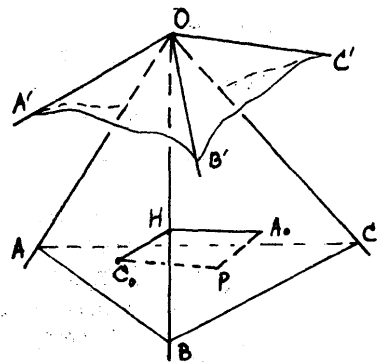圖3

設在三面角O-ABC的內部選一點P，過P作OA'的平行線交平面(BOC) 於A₀，即有PA₀⊥(BOC)；又過P作OC'的平行線交平面(AOB)於C₀，即有PC₀⊥(AOB)；並且∠A₀PC₀=∠A'OC'。

又設平面(PA₀C₀)與OB交於H，因PA₀⊥OB，PC₀⊥OB，故OB⊥(PA₀C₀)，於是OB⊥ A₀H，OB⊥C₀H，即∠A₀HC₀為二面角A-OB-C的一個平面角。

在四邊形PA₀HC₀中，因∠HA₀P=∠HC₀P=90°，所以∠A₀PC₀與∠A₀HC₀互補。

即面角∠A'OC'與二面角A-OB-C互補。

同理可證其餘的面角與相應的二面角互補。