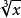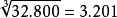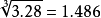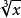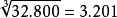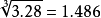表算

表算是特殊的計算方法之一，指利用已經製作好的數表，用查表的方法進行計算。例如利用平方根表求平方根；利用對數表進行計算等。

基本介紹

• 中文名：表算
• 所屬學科：數學
• 簡介：利用各種數學用表進行的計算
• 相關概念：立方表，立方根表，對數表等

定義

表算指利用各種數學用表進行的計算。例如利用立方根表求立方根；利用對數表進行計算等。

表算舉例

利用立方根表求立方根

基本介紹

立方根表是常用數表之一，即一元實函式的函式值表。立方根表有多種，其查法不盡相同，一般在表後給以說明。例如，在四位數學用表的立方根表中能直接查出0.100到99.9間的三位數的立方根。對於不能直接查出的實數x，可將其寫成的形式，即

為從0.100到99.9之間的三位數，然後從立方根表中查出的值，最後通過計算得出的值。根據考古發掘出來的古代巴比倫人的泥板書(粘土書板)的記載，大約公元前2100多年，由於農業和商業的發展，泥板書中就刻有立方根表，並用於有關立方體的計算。

注意事項與使用

1．由《立方根表》能查出任意一個三位數的立方根，0.100到99.9之間的三位數（表內數）的立方根可以在表上直接查出，如

2．小於0.1或大於99.9的數的立方根在表上不能直接查得，要先移動被開方數的小數點，使它成為表內可以查到的數。移動小數點時必須三位三位地移，如

被開方數32800，先要移成32.800；

被開方數0.00328，先要移成3.28；

被開方數328000，先要移成0.328。

3．查表前被開方數的小數點每移三位，查得的立方根的小數點要向相反方向移一位。

例： 查

解：因為， 所以；

因為， 所以；

因為， 所以

4．被開方數有三個數位以上的，先四捨五入，再查表。

5．立方根表沒有修正值。

6．開方結果是否正確，可用乘方方法進行檢驗。

7.分數要化成小數查表。

利用平方表求平方

概念

平方表(table of squares)是常用數表之一，即一元實函式的函式值表。平方表有多種，一般其具體查法將在表後說明，利用常見的四位數學用表的平方表可查出任意一個四位數的平方數，1到10之間的四位數可在表中直接查出。對小於1或大於10的正實數x不能在表中直接查出，要首先將它寫成(為四位數)的形式，即，然後在表中查出的值，最後通過計算得出x的值。

平方表使用說明

在生活或工農業生產或科學實驗中，為了解決手算平方計算比較麻煩，所編制的能直接查到四位數平方的一種表格。

平方表的使用說明：

1．表的左上角標有N字。N的最左直列是所查四位底數的前兩個數字(1.0到9.9)，N的最上或最下一橫行是底數的第三個數字(0.01到0.09)。所查的直列與橫行相交處。就是前位的平方冪。如2.46²=6.052。

2．修正值的查法：雙縱線後最上或最下一橫行是所查底數的最末一位數(0.001到0.009)。查四位數的平方，要把前三位數的平方同第四位數所對應的修正值相加。

例：查表求2.468的平方．

解：因為2.46²=6.052，0.008的修正值是0.039所以2.468²=6.052+0.039=6.091。

3．小於1或大於10的數的平方，在表上不能直接查到。要先移動小數點的位置，使查的數在表上能直接查到。查表前的小數點若移動幾位時，查得的平方數的小數點要向相反方向移動2n位。

例：查表求246.8，0.2468的平方。

解：246.8²=60910． (要查246.8²，需查2.468²=6.091，小數點向左移動2位，結果要反向移動2n位，即反向移動向右移4位)。

解：0.2468²=0.06091．(要查0.2468²，需查2.468²=6.091，小數點向右移1位，結果要反向移動2n位，即反向移動向左移2位)。

利用立方表求立方

概念

一元實函式的函式值表叫做立方表，其中。

運用立方表，可求出任一正實數x的立方值，這只須把x表成形式，其中，n是整數，而，這裡的值可從立方表直接查得。

立方表的使用說明

立方表是為了解決立方計算更加繁瑣，所編制能直接查到四位數立方的一種表格。

立方表的使用說明：

1．查前三位數的立方同於查平方表的說明1。

2．修正值的查法：雙縱線後最上或最下一橫行是查底數的是最末一位數(0.001到0.009)。但只有五個數碼1、2、3、4、5，若5以內的數，修正值方法用於平方的修正值法。若在6至9間的修正值，則在查第三位時加上1，再去修正值。如是6就減4的修正值。

例：查表求5.193．5.197的立方。

解：5.193³=139.8+0.2=140.0，

5.1973=140.6-0.2=140.4(先查5.20的立方結果是140.6，再減去0.003的修正值0.2)。

3．小於1或大於10的數點的立方，在表上不能直接查到。要先移動小數點的位置，使查的數在表上能直接查到。查表前的小數點若移動n位時，查得的立方冪的小數點要向相反方向移動3n位。

例：查表求51.93，0.05197的立方。

解：因為5.193³=140.0，

所以51.93³=140000．(要查51.93，需查5.193，小數點左移1位。把查得的結果140.0的小數點向右移3位，得140000)

解：因為5.197³=140.4．

所以0.05197³=0.0001404． (要查0.05179，需查5.197，小數點左移2位。把查的結果140.4的小數點向左移6位，得0.0001404)。

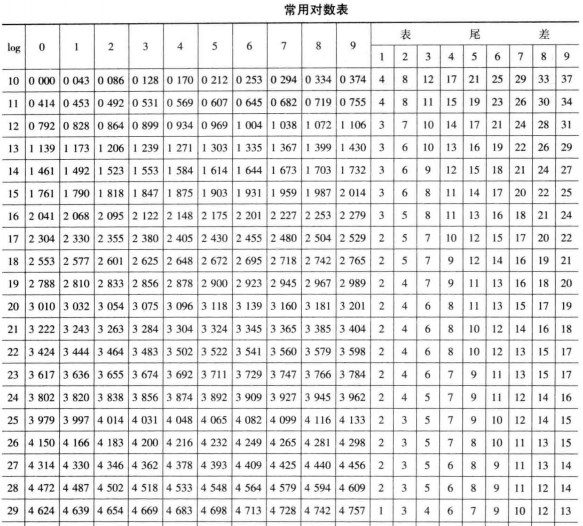
利用對數表求對數

對數表(logarithm table)是一種常用的數表，指常用對數表和自然對數表。函式y=lg x的函式值表稱為常用對數表。實際上，表中只列出真數x(1≤x<10)的對數尾數的準確值或近似值，因而這樣的表也稱為常用對數尾數表。表中不列出首數，它由常用對數的性質確定，真數和對數尾數的精確度取決於對數表的位數，位數越多，精確度越高。如果真數和對數尾數都列出四個有效數字，則稱為四位常用對數表；如果列出五個有效數字，則稱為五位常用對數表。歷史上，由於常用對數在數值計算中的巨大作用，有許多人投入了編制對數表的工作。布里格斯(H.Briggs)於1617年，首先發表1-100的至小數點八位的常用對數表，1624年，在他的《對數算術》中發表1-20000及90000—100000的至小數點14位的常用對數表，其中20000—90000的常用對數表是在弗拉克(A.Vlacq)的幫助下於1628年編制並發表的.函式y=ln x的函式值表稱為自然對數表，習慣上的對數表一般指常用對數表。