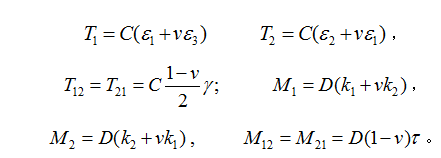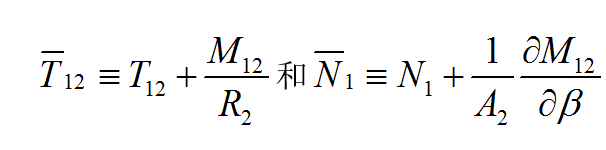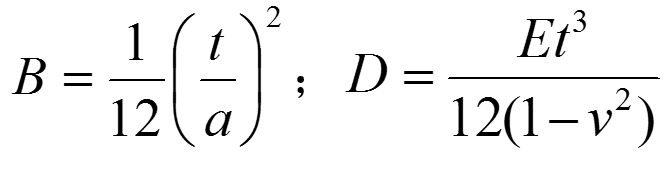基本介紹
所謂殼體是由內、外兩個曲面圍成的物體,兩個曲面稱為殼體的表面。與兩個曲面等距的點所形成的曲面稱為殼體的中面;兩曲面之間的中面法線長度稱為殼體的厚度。一般殼體可用中面的幾何形狀和厚度來描述。中面封閉的殼體稱為封閉殼體,否則稱為開口殼體。開口殼體除了內外表面外,還有四周的邊界面。最大厚度遠小於中面曲率半徑和另外兩個方向尺寸的殼體稱為薄殼。薄殼主要以沿厚度均勻分布的中面
應力而不是以沿厚度變化的彎曲應力來承受外載,具有重量輕、
強度高的優點,所以在航天、航空、造船、化工、建築、水利和機械等工業中得到廣泛套用。
 相關圖書
相關圖書薄殼理論是19世紀末在基爾霍夫-樂甫假設的基礎上建立起來的。進入20世紀後,在生產技術的推動下,殼體理論曾有較大的發展。當時主要是針對不同類型的殼體建立各種簡化理論。50年代開始對基爾霍夫-樂甫假設進行修正,使薄殼理論精確化。隨著電子計算機的進步,薄殼理論在數值計算以及理論分析和數值計算相結合兩方面都有迅速發展。
基本理論
薄殼的幾何形狀和變形情況通常都很複雜,必須引入一系列簡化假設才能進行研究。最常用的假設是基爾霍夫-樂甫假設,以此為基礎可建立薄殼的微分方程組,通過解微分方程組可得到殼體中的位移和應力。
基爾霍夫-樂甫假設 1874年德國的H.阿龍將
薄板理論中的基爾霍夫假設推廣到殼體。1888年經英國的A.E.H.樂甫修正,形成至今仍然廣泛採用的薄殼理論。基爾霍夫-樂甫假設包括四個內容:①殼體厚度(
t)遠小於中面最小曲率半徑
R; ②殼體的變形和位移量都非常小,而且轉角和
應變是同級小量,在變形幾何關係中可以忽略二次以上的高階項;③中面法線方向的正應力分量遠小於與法線垂直方向上的正應力分量,前者在應力-應變關係中可略去不計;④變形前中面的法線在變形後仍為
法線,且在變形過程中,殼體厚度不變。嚴格地說,③和④兩點假設是不相容的,不過由此引起的誤差在
t/
R量級以內,這對薄殼來說是允許的。
 相關圖書
相關圖書薄殼中的變形和內力 相應於基爾霍夫-樂甫假設的薄殼的中面變形包括兩個正交方向(α、β方向)的中面正應變ε1、ε2,中面剪應變γ,兩個方向的中面曲率變化κ1、κ2和中面扭率變化值κ12;薄殼中的中面內力包括法向力T1、T2,切向力T12、T21,橫向剪力N1、N2,彎矩Μ1、Μ2和扭矩Μ12、Μ21(見圖)。薄殼理論的任務就在於求出中面的變形和內力,進而根據下列表達式求出殼內的應變分量和應力分量σ1、σ2、τ12:
式中z為所考慮的點到中面的距離。上述諸式中等號右端的第一項為沿厚度均勻分布的薄膜應變和應力,第二項為線性分布的彎曲或扭轉應變和應力。
基本方程
根據彈性力學並利用
基爾霍夫-樂甫假設建立起來的近似理論稱為殼體的樂甫一級近似理論。它包含一系列基本方程:
①應變-位移關係式 套用微分幾何中的曲面理論,中面變形的應變-位移關係式(即幾何方程)為:
式中u、v、w為沿α、β方向和法方向的位移分量;A1、A2為 α、β方向的拉梅係數;R1、R2為α、β方向的曲率半徑。由於曲率的存在,殼體變形中的切向位移分量u、v與法向位移分量ω間便有耦合關係,從而造成殼體幾何方程的複雜化。
②靜力平衡方程 它的一般形式可寫為:
式中
q1、
q2和
q3分別為單位中面面積上在
α、
β方向和法方向的表面載荷分量。這些方程表明,中面切向的平衡方程中包含橫向剪力
N1和
N2,而在法向的平衡方程中又含有中面內力
T1和
T2。即使在小變形情況下,中面內力與橫向剪力也是相互
耦合的。此外,最後一式按內力定義應為恆等式。
 相關圖書
相關圖書③應力-應變關係 反映殼體內中面內力和應變之間的關係,即
式中
C =
Et/(1-
v2),v為
泊松比,E為
彈性模量;D=Et3/12(1-v2),稱為彎曲剛度。
求解殼體內的位移和內力須將上述各方程聯立。上述聯立基本方程組可化為僅用殼體的
撓度表達的八階
偏微分方程。從理論上講,只要有足夠的邊界條件,即可以從這些方程中解得全部未知量。一般說來,在每個邊界上只能有四個邊界條件,但自然邊界條件有五個。在這種情況下,應將扭矩化為等效的剪力,譬如在邊界上,兩個剪內力化為:
理論套用
殼體方程組十分複雜,所以對任意載荷下的任意形狀殼體求得一般解是很困難的,而只能求經過簡化的某些特殊殼體的解,它們在工程套用上具有重要的價值。這些殼體有:
薄膜殼
如果殼體的幾何形狀(包括厚度)和表面載荷都是連續可微函式,則除殼體邊緣局部區域可能由於受支承而出現彎曲應力外,大部分殼體一般處於無彎矩的應力狀態。這種狀態與薄膜受力狀態相當,可根據殼體的無矩理論求解。按照這個理論,彎矩分量Μ1=Μ2=Μ12=0。根據平衡條件得到N1=N2=0;T12=T21,記為S。這樣,在一般情況下,殼體的六個平衡方程將簡化成只包含三個未知內力的三個方程:
無矩理論的上述基本方程是靜定可解的,並且可歸結為某個位移函式(見
應力函式和位移函式)的四階偏微分方程。工程上常見的二次旋轉曲面殼體,在軸對稱載荷(如均布壓力、水壓、風型載荷和重力等)作用下,可用無矩理論求得解析解。該解不僅近似地反映了殼體大部區域的應力和變形,而且在一般情況下,它與考慮彎矩後得到的特解之差為
t/
R的數量級,故可近似地作為特解。此外,無矩狀態還是結構最佳的受力狀態,所以無矩理論具有重要的實用價值。
圓筒殼
圓筒殼製作方便,套用極為廣泛。此外,圓筒殼沿母線方向的曲率為零,而其周向曲率又為常數,所以易於進行理論分析。最初,圓筒殼方程的表達式相當複雜,1933年美國的L.H.唐奈作了簡化:①在殼體中面的周向平衡方程中,忽略周向曲率對橫向剪力
N2的影響;②在變形分量κ1、κ2和κ12的幾何方程中,略去含切向位移分量
u和
v的項。由此得到在僅有法向表面載荷
q3作用的唐奈方程: 式中
ξ=
x/
a,
θ=
s/
a,
a為圓筒的半徑,
x、
s分別表示軸向和周向的長度變數;
為拉普拉斯算符。對於較短的圓柱殼,唐奈方程具有一定的精度。1959年美國的F.W.莫利對唐奈方程作了改進,他將第三個法向位移方程改成下式:從而提高了唐奈方程的精度並擴大了它的套用範圍,形式也得到了簡化。對軸對稱載荷作用下的圓筒殼,唐奈方程簡化為彈性基礎上板條梁的彎曲方程。

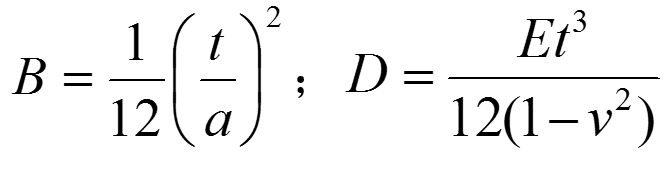
1932年,蘇聯的В.З.
符拉索夫針對周向加勁的長圓柱殼體(見
加勁板殼)提出了一種簡化的半無矩理論(又稱半彎矩理論)。它是在忽略柱體母線方向所有彎矩和周向變形的基礎上建立的理論,它還被推廣套用於任意截面形狀的長柱殼體。
旋轉殼
德國的H.瑞斯納和瑞士的E.邁斯納分別於1912年和1913年以旋轉殼體經線上的橫向剪力和緯線方向的主曲率半徑的積作為變數,並用經線上切線的轉動角為另一變數,將殼體基本方程簡化成兩個互相耦合的二階常微分方程的方程組。在無表面載荷的情況下,它是齊次方程組,可化為一個複數函式表達的二階常微分方程。由於殼體彎曲具有邊界效應,作為初級近似,德國的J.W.蓋克勒於1926年曾利用這一特點把方程進一步簡化。因原微分方程具有漸近性質,所以可用漸近積分方法求得精度較高的解。
扁殼
對於工程上常用的拱高較小(一般拱高與底面特徵長度相比不超過1/5)的扁殼,德國的K.馬格雷和蘇聯的穆什塔利於1938年根據其幾何特點分別建立了這類殼體的基本方程。1944年符拉索夫將這一成果發展成為系統的扁殼近似理論。這一理論利用殼體中面扁平的特點把高斯曲率近似地取為零。另外,除了在中面應變分量的幾何關係式和法向平衡方程中保留曲率效應外,其他都近似地採用平板方程的表達式。由於這些簡化和圓柱殼體中的唐奈方程的近似假定相同,扁殼理論套用於零高斯曲率的圓柱殼體同唐奈方程完全一致,因此扁殼方程也可以說是唐奈方程的推廣。
 相關圖書
相關圖書 相關圖書
相關圖書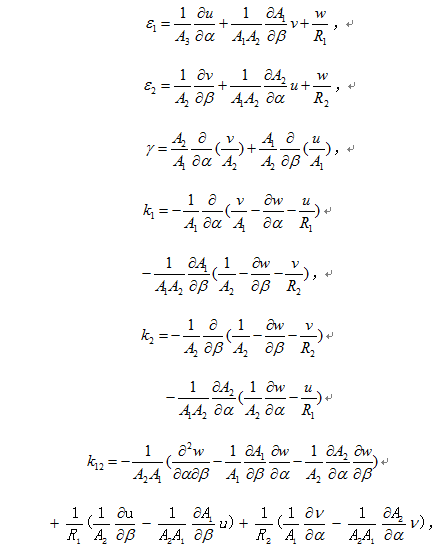
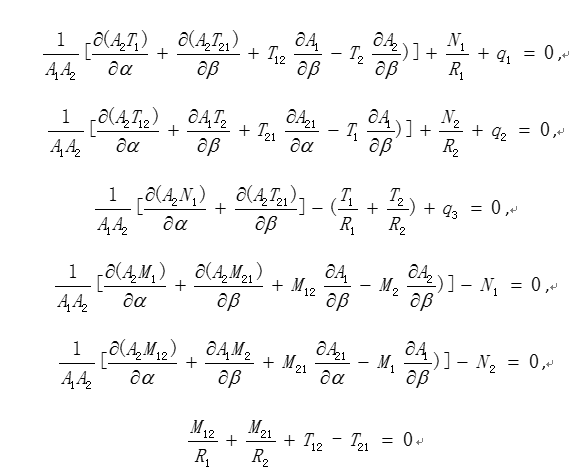
 相關圖書
相關圖書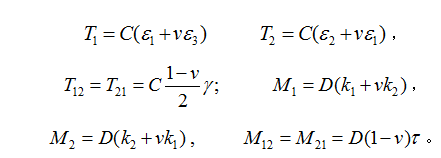
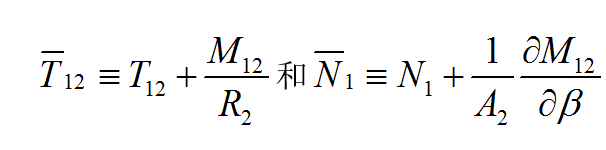



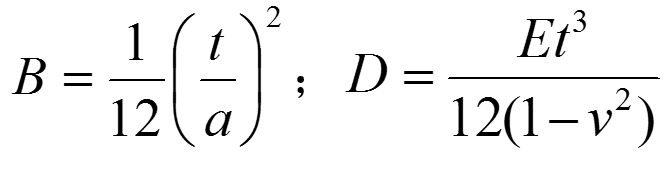
 相關圖書
相關圖書 相關圖書
相關圖書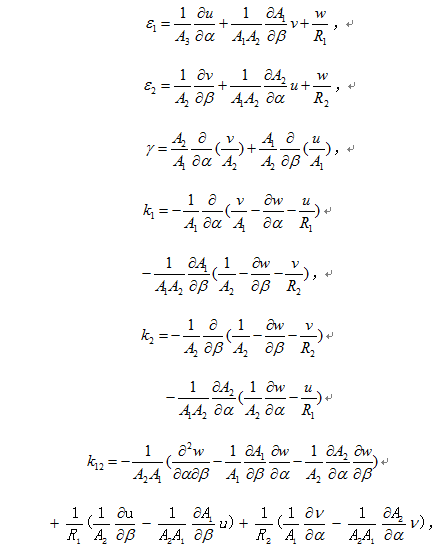
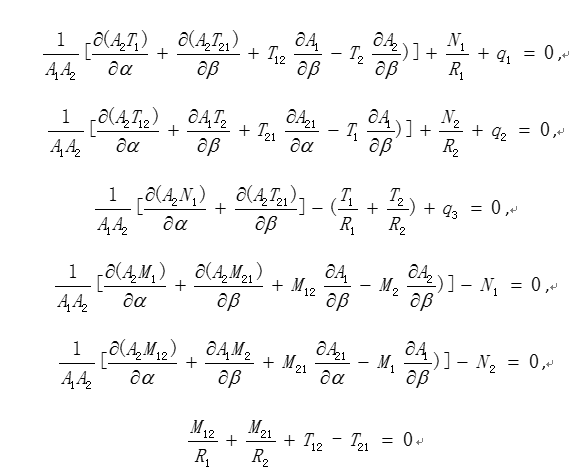
 相關圖書
相關圖書