基本介紹
- 中文名:蓋帽模型
- 外文名:Gap models
簡介
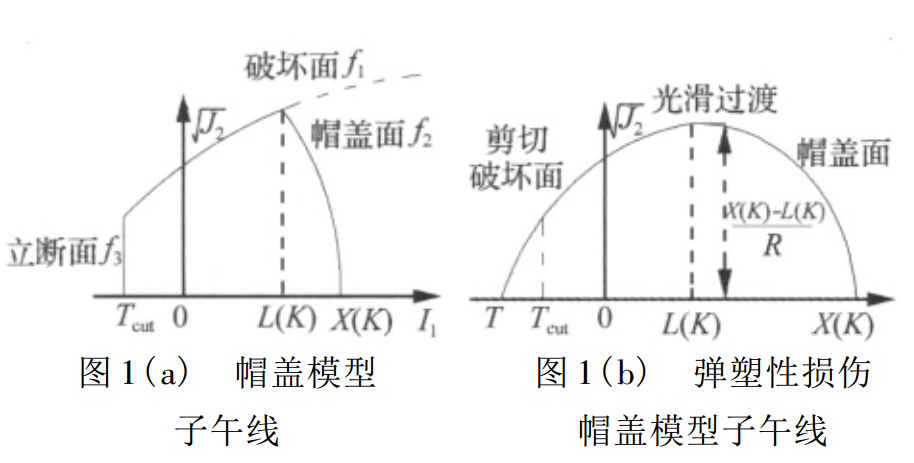
蓋帽模型的發展

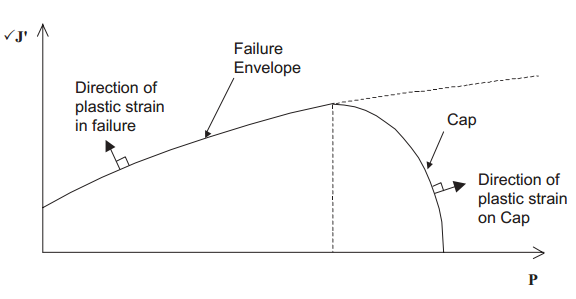
廣義蓋帽模型



帽蓋參數確定











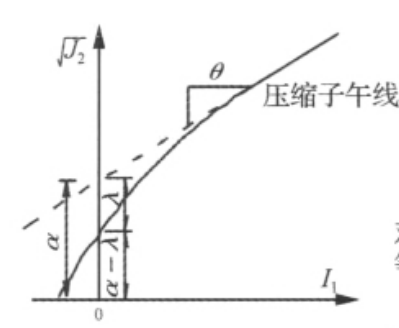
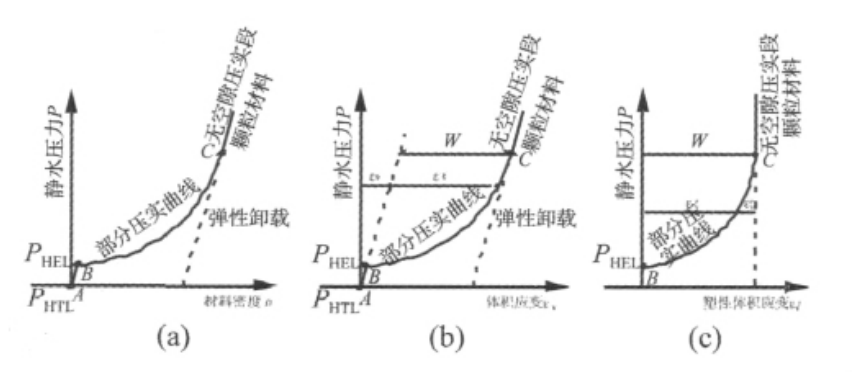
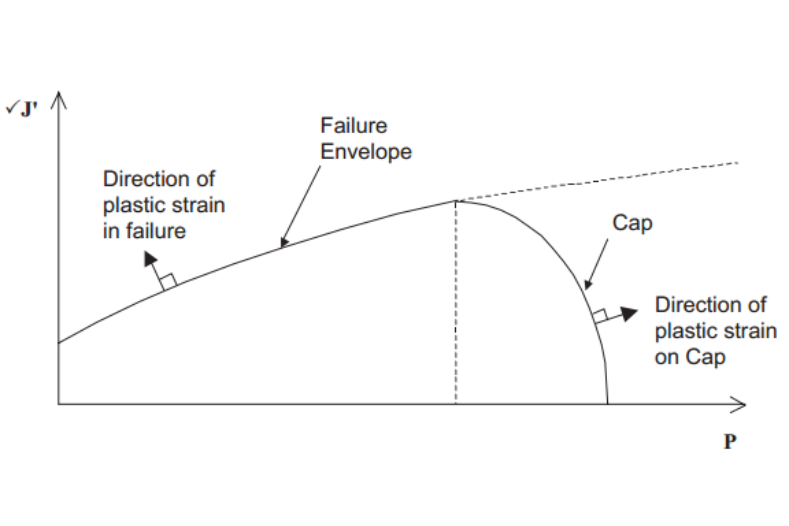



















帽蓋模型是描述地質孔隙介質彈塑性破壞特徵的重要工具之一。蓋帽模型又可叫帽蓋模型(Cap models),該模型提供了一種強大的、可適應的方式,可代表地質材料的動態應力應變行為的許多方面。蓋帽系列模型已經被廣泛套用了30多...
方蓋帽注塑模 防護罩注塑模 ……附錄A 常用熱塑膠主要性能特點和工藝參數 附錄B 常用塑膠材料的成型推薦值及其應考慮的問題 附錄C 注塑材料的共注相容性 附錄D 注塑模具常用鋼材 附錄E 注塑模具流道直徑估算值 附錄F 模具問題對工藝和...
(4) 劉志林,孫巍巍,王曉鳴,馮君,基於蓋帽模型的混凝土動態球型空腔膨脹模型和侵徹阻力分析,兵工學報,2015.12.15,(12):2209~2216,EI,北大中文核心期刊 (5) 程奇鵬,孫巍巍,盧賽,基於PFC3D的淺圓倉偏心卸料離散元研究,土木...
1.排球大帽(防守、蓋帽)長谷川高高躍起,以排球扣殺的姿勢,送給對手一個超級大帽。對方出手時,點擊“排球大帽”按鍵。2.閃電封蓋(防守、蓋帽)只要長谷川位於投籃者的防守區域內,會閃電般的跳起封蓋對手的投籃。對方出手時,在...
1.抓球蓋帽(防守、蓋帽)魚住純伸展雙臂,高高躍起,將對手所投出的球,直接抓在手裡。對方出手時,點擊“抓球蓋帽”按鍵。2.長臂蓋帽(防守、蓋帽)魚住純超長的臂展,擁有更遠的蓋帽範圍,能輕鬆向對手的投籃進行封蓋。對方出手...
空中自由風格讓你的比賽前所未有地充滿炫目的扣籃、空中接力、補籃和極具破壞性的蓋帽。無論是高高躍起扣籃還是獨門自由風格花式運球和假動作都使你在球場上獲得更好的操控感。當真實的球員動作和改良的場上布局讓你沉浸在NBA快速激烈...
把熔煉的鋼水澆入模型,冷卻凝固而成的鋼塊是製造各種鋼材的原料。鋼錠縮頭是只經過了最基本(最低限)的脫氧處理。定義 鋼錠縮頭凝固時,鋼錠縮頭模的四周及底部生成一層接近純鐵的金屬層,而碳、硫及磷等則於中央收縮孔附近生成偏...
6.蒙眼蓋帽(防守、蓋帽)面對來不及封蓋的正面投籃,池上亮二會伸手封堵對手視線,影晌對手投籃。對方出手時,點擊“蒙眼蓋帽”按鍵。玩法分析 1、天賦效果 參考資料來源。2、潛能搭配 進攻大前:完美防守、投籃封鎖、沖搶籃板、強力...
2.飛人蓋帽(防守、蓋帽)清田信長超強的敏捷和彈跳力,讓其如同飛人般,跳起進行封蓋。對方出手時,點擊“飛人蓋帽”按鍵。3.後撤瞬突(技巧、突破)清田信長向後撤步蓄力,瞬間爆發超強的速度,直接突破對手。傳持球進攻時,點擊“後...
中投+0.5/1/1.5/2/3;蓋帽+0.2/0.3/0.5/0.7/1;空位中投+0.7%。 強力蓋帽 蓋帽+0.5/1/1.5/2/3;力量+0.2/0.3/0.5/0.7/1;扣籃撞倒+0.7%。 籃板中鋒:卡位的目的、空中戰鬥、完美防守、穩定中投、籃下悍將、超級籃板 潛能名稱 ...
福田吉兆的使用高拋的姿勢,投出難以封蓋的高拋球,完成上籃。5.進攻速板(防守、籃板)福田吉兆在面對進攻籃板時,面對身前的籃板,會一瞬間快速跳跳起搶到籃板。6.更多的歡呼(被動、投籃)福田吉兆渴望得到更多的歡呼,隨著得分越多...
6.野蠻蓋帽(防守、蓋帽)內藤鐵也如同野獸般跳起,野蠻的將對手的投籃扇飛。對方出手時,點擊“野蠻蓋帽”按鍵。玩法分析 1、天賦效果 參考資料來源。2、潛能搭配 進攻大前:完美防守、投籃封鎖、沖搶籃板、強力近投、內線干擾、精準傳...
防守大前:完美防守、投籃封鎖、沖搶籃板、快速恢復、內線屏障、強力蓋帽 均衡大前:完美防守、投籃封鎖、沖搶籃板、強力近投、內線屏障、超級籃板、穩定中投、籃下悍將、強力蓋帽 參考資料來源。3、羈絆搭配 籃下雙雄(二人羈絆組):...
6.飛身蓋帽(防守、蓋帽)仙道彰衛狀態下,敏銳的洞察力,會在對手投籃時,飛身封蓋對手。對方出手時,點擊“飛身蓋帽”按鍵。玩法分析 1、天賦效果 參考資料來源。2、潛能搭配 進攻小前:永不言棄、突襲者、腳踝終結者、穩定中投、...
6.跑動蓋帽(防守、蓋帽)村雨健吾加速中飛身跳起,能夠封蓋更遠投籃的對手。對方出手時,跑動狀態下,點擊“跑動蓋帽”按鍵。玩法分析 1、天賦效果 參考資料來源。2、潛能搭配 進攻小前:永不言棄、突襲者、腳踝終結者、穩定中投、...
2.拍蒼蠅(防守、蓋帽)赤木剛憲施展拍蒼蠅絕學,將對手的投籃直接蓋飛。對方出手時,點擊“拍蒼蠅”按鍵。3.夢幻舞步(進攻、投籃)赤木剛憲在籃下施展夢幻舞步,晃過對手,完成投籃。技能施放區域,點擊“夢幻舞步”按鍵。4.赤木籃板...
