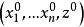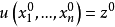蒙日方程

在偏微分方程的數學理論中，以Gaspard Monge命名的蒙日方程是獨立變數x1，...，xn中未知函式u的一階偏微分方程，叫蒙日方程。

基本介紹

• 中文名：蒙日方程
• 外文名：Monge equation
• 學科：數學
• 提出者：蒙日
• 性質：偏微分方程
• 相關名詞：蒙日-安培方程

簡介

在偏微分方程的數學理論中，以Gaspard Monge命名的蒙日方程是獨立變數x1，...，xn中未知函式u的一階偏微分方程。

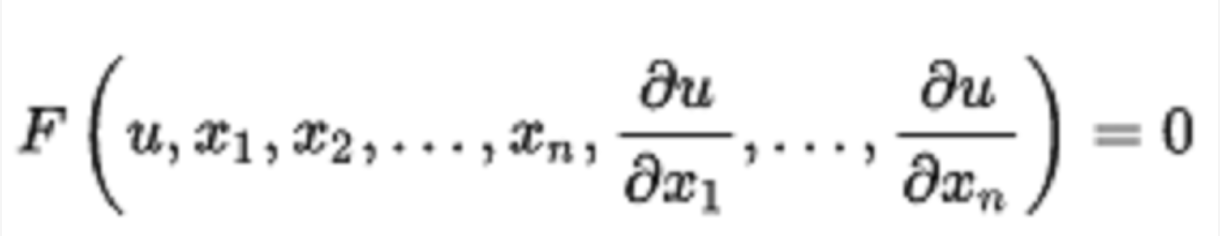
這是u的偏導數中的多項式。 任何蒙日方程都有一個蒙日錐。

通常，將u = x0，寫入程度為k的蒙日方程式：

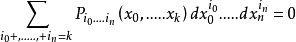
並表示差分dx_k之間的關係。 給定點（x0，...，xn）上的蒙格錐是該點切線空間中的方程的零軌跡。

蒙日方程與（二階）蒙日-安培方程無關。

蒙日錐（Monge cone）

在偏微分方程（PDE）的數學理論中，蒙日錐是與一階方程相關聯的幾何對象。 它被命名為Gaspard Monge。 在兩個方面，讓

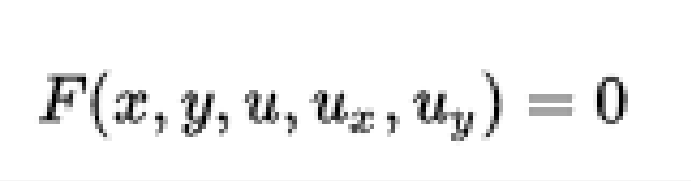
作為兩個變數x和y中的未知實值函式u的PDE。 假設這個PDE是非退化的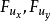，在定義域中既不為零， 修正一個點（x0，y0，z0）並考慮具有的解函式u

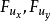
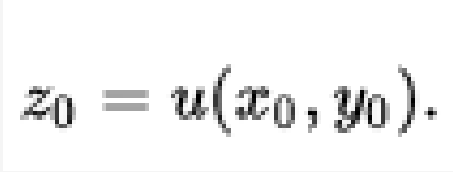
（1）滿足（2）的每個解確定圖形的切平面

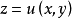
通過點（x0，y0，z0）。 隨著對（ux，uy）求解（1）的變化，切平面包圍在R3中具有頂點（x0，y0，z0）的圓錐，稱為蒙日錐。 當F為準線性時，蒙日錐退化為稱為蒙日軸的單線。 否則，蒙日錐體是一個適當的錐體，因為通過固定點的平面和非同軸單參數系列的平面包圍錐體。 顯然，原始偏微分方程在R3的餘切束上產生一個標量值函式，在一個點（x，y，z）上由

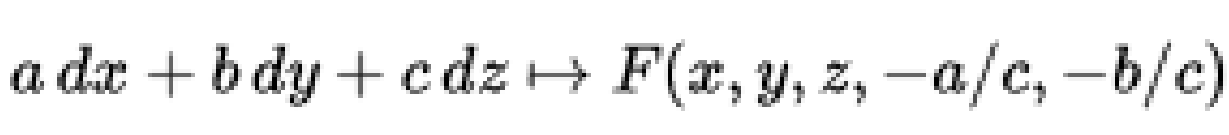
F的消失決定投影平面中具有均勻坐標（a：b：c）的曲線。 雙曲線是該點的投影切線空間中的曲線，該曲線上的仿射錐是蒙日錐。 錐體可以具有多個分支，每個分支在投影切線空間中的簡單閉合曲線上具有仿射錐。

當基點（x0，y0，z0）變化時，錐體也會變化。 因此，蒙格錐是R3上的錐形場。 因此，（1）的尋找解可以被解釋為在該點處找到與蒙日錐相切的表面。 這是特徵的方法。

該技術推廣到n個空間變數中的標量一階偏微分方程；即，

通過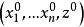，蒙日錐（或準線性情況下的軸）是PDE與。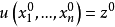