莖葉圖（Stem-and-Leaf display）又稱“枝葉圖”，是在20世紀早期由英國統計學家阿瑟·鮑利（Arthur Bowley）設計，1977年統計學家約翰托奇（John Tukey）在其著作《探索性數據分析》（exploratory data analysis）中將這種繪圖方法介紹給大家，從此這種作圖方法變得流行起來。
基本介紹
- 中文名：莖葉圖
- 外文名：stem-and-leaf display
- 別稱：枝葉圖
- 特徵：方便記錄
- 數據：可判斷中位數
- 特殊工具：與直方圖相似
簡單介紹,與直方圖的比較,優缺點,優點,缺點,例子,例1,例2,找中位數,
簡單介紹
莖葉圖的思路是將數組中的數按位數進行比較，將數的大小基本不變或變化不大的位作為一個主幹（莖），將變化大的位的數作為分枝（葉），列在主幹的後面，這樣就可以清楚地看到每個主幹後面的幾個數，每個數具體是多少。
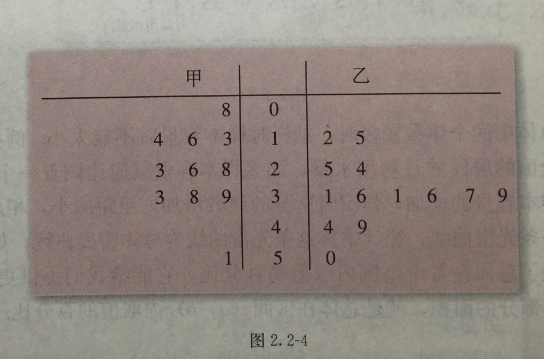
莖葉圖有三列數：左邊的一列數統計數，它是上（或下）向中心累積的值，中心的數（帶括弧）表示最多數組的個數；中間的一列表示莖，也就是變化不大的位數；右邊的是數組中的變化位，它是按照一定的間隔將數組中的每個變化的數一一列出來，像一條枝上抽出的葉子一樣，所以人們形象地叫它莖葉圖，如圖1所示。
圖1 莖葉圖與直方圖的比較
莖葉圖是一個與直方圖相類似的特殊工具，但又與直方圖不同，莖葉圖保留原始資料的資訊，直方圖則失去原始資料的訊息。將莖葉圖莖和葉逆時針方向旋轉90度，實際上就是一個直方圖，可以從中統計出次數，計算出各數據段的頻率或百分比。從而可以看出分布是否與常態分配或單峰偏態分布逼近。
莖葉圖在質量管理上用途與直方圖差不多，但它通常是作為更細緻的分析階段使用。由於它是用數字組成直方圖，所以在做的時候比直方圖時，通常我們常使用專業的軟體進行繪製。
優缺點
優點
1、用莖葉圖表示數據有兩個優點：
（1）從統計圖上沒有原始數據信息的損失，所有數據信息都可以從莖葉圖中得到；
（2）莖葉圖中的數據可以隨時記錄，隨時添加，方便記錄與表示。
缺點
莖葉圖只便於表示個位之前相差不大的數據，而且莖葉圖只方便記錄兩組的數據。兩個以上的數據雖然能夠記錄，但是沒有表示兩個記錄那么直觀、清晰。
例子
例1
下面有一堆數據共30個：
89、79、57、46、1、24、71、5、6、9、10、15、16、19、22、31、40、41、52、55、60、61、65、69、70、75、85、91、92、94
畫出的莖葉圖如下：
莖|葉
0 | 1 5 6 9
1 | 0 5 6 9
2 | 2 4
3 | 1
4 | 0 1 6
5 | 2 5 7
6 | 0 1 5 9
7 | 0 1 5 9
8 | 5 9
9 | 1 2 4
比如第二行的數字：
1 | 0 5 6 9，
它們代表數據集中有10、15、16和19四個數字。
可以這樣理解莖+葉=實際的數值，如 1|0 5 6 9 中莖值為1，葉值為 0、5、6和9共四個葉值。
其真實數值計算方式：莖值連線葉值，也就是說當莖值是1，葉值是0時，連線起來就是真實數值10。
例2
現在有一堆30個數據：
41、52、6、19、92、10、40、55、60、75、22、15、31、61、9、70、91、65、69、16、94、85、89、79、57、46、1、24、71、5
畫出的莖葉圖如下：
0 | 1 5 6 9
1 | 0 5 6 9
2 | 2 4
3 | 1
4 | 0 1 6
5 | 2 5 7
6 | 0 1 5 9
7 | 0 1 5 9
8 | 5 9
9 | 1 2 4
比如第二行的數字如下：
1 | 0 5 6 9
則代表數據集中有10、15、16和19四個數字。
41、52、6、19、92、10、40、55、60、75、22、15、31、61、9、70、91、65、69、16、94、85、89、79、57、46、1、24、71、5
畫出的莖葉圖如下：
0 | 1 5 6 9
1 | 0 5 6 9
2 | 2 4
3 | 1
4 | 0 1 6
5 | 2 5 7
6 | 0 1 5 9
7 | 0 1 5 9
8 | 5 9
9 | 1 2 4
比如第二行的數字如下：
1 | 0 5 6 9
則代表數據集中有10、15、16和19四個數字。
注意：一個莖可以有很多葉也可以不出現葉。
找中位數
舉個例子，如圖2所示，列出數：2、10、15、20、23、27。中間的數是（15+20）/2=17.5，即17.5為中位數，假如中間加上一個數22，中位數則變成了20。
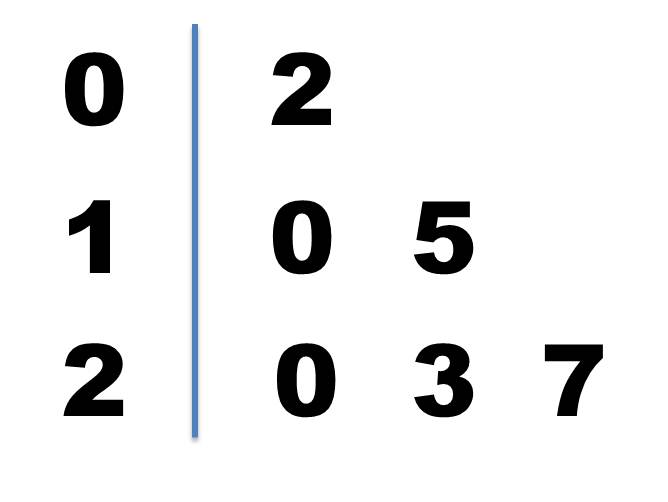圖2找中位數