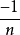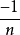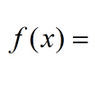艾森斯坦因判別法

艾森斯坦判別法是代數的定理，給出了判定整係數多項式不能分解為整係數多項式乘積的充分條件。由高斯定理，這種好用的判別法也是多項式在有理數域不可約的充分條件。

基本介紹

• 中文名：艾森斯坦因判別法
• 外文名：Eisenstein's irreducibility criterion
• 表達式：多項式
• 提出者：Ferdinand Gotthold Max Eisenstein 
• 套用學科：數學
• 適用領域範圍：整係數多項式

定理定義

艾森斯坦判別法是說：給出下面的整係數多項式f(x)=a_nxⁿ+a_n-1x^n-1+…+a₀

如果存在素數p，使得

p不整除a_n ，但整除其他a_i,(i=0,1,...,n-1) ；

p² 不整除a₀ ，

那么f(x) 在有理數域上是不可約的。

套用例子

給了多項式g(x) = 3x²+ 15x + 10，試確定它能否分解為有理係數多項式之積。

試用艾森斯坦判別法。素數2和3都不適合，考慮素數p = 5。5整除x的係數15和常數項10，但不整除首項3。而且5² = 25不整除10。所以g(x)在有理數域不可約。

有時候不能直接用判別法，或者可以代入y = x + a後再使用。

例如考慮h(x) = x²+ x + 2。這多項式不能直接用判別法，因為沒有素數整除x的係數1。但把h(x)代入為h(x + 3) = x² + 7x + 14，可立刻看出素數7整除x的係數和常數項，但7²= 49不整除常數項。所以有時通過代入便可以用到判別法。

艾森斯坦判別法得出的一個著名結果如下：

對素數p，以下多項式在有理數域不可約。

要使用艾森斯坦判別法，先作代換x = y + 1。新的常數項是p，除首項是1外，其他項的係數是二項式係數，k大於0，所以可以被p除盡。

驗證推導

對多項式f(x)取模p，也就是把它的係數映射到整數模P的環上。這樣它便化為f（x）≡cxⁿ,0<c<p,c為非零常數。因為在域上的多項式有唯一分解，f在模p上會分解為單項式。

如果f是在有理數上可約的，那么會有多項式g, h使得f = g×h。從上可知g和h取模p分別為dx^k和ex^n-k，滿足c = d×e。因為g和h模p的常數項為零，這表示g和h的常數項均可被p整除，所以f的常數項a₀可以被p₂整除，與f係數的假設矛盾。因此得證。

進一步解釋

依據牛頓圖的理論在其p進制數域，我們考慮一系列點的下凸集。

(0,1), (1, v₁), (2, v₂), ..., (n − 1, v_n-1), (n,0), 其中v_i 是a_i 關於p的最高次冪。對於一個艾森斯坦多項式，

對0 < i < n,v_i≥1，v₀ =1 v_n =0, 固而它的牛頓圖即點列的下凸集應當是一條從(0,1)到(n,0)的線段，其斜率為