舞會問題(problem of dance)亦稱婚姻問題或工作安排問題,是一類組合問題。設有n個男子和n個女子,每個男子與n個女子中的若干個互相認識,問這些男子和女子能否結成n對夫婦,使每對夫婦都是已經相互認識的。
基本介紹
- 中文名:舞會問題
- 外文名:problem of dance
- 所屬學科:數學(組合學)
- 別稱:婚姻問題或工作安排問題
基本介紹
荷爾的婚姻定理

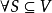
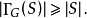
舞會問題的解答




舞會問題(problem of dance)亦稱婚姻問題或工作安排問題,是一類組合問題。設有n個男子和n個女子,每個男子與n個女子中的若干個互相認識,問這些男子和女子能否結成n對夫婦,使每對夫婦都是已經相互認識的。

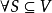
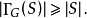



舞會問題(problem of dance)亦稱婚姻問題或工作安排問題,是一類組合問題。設有n個男子和n個女子,每個男子與n個女子中的若干個互相認識,問這些男子和女子能否結成n...
舞會是西方一種正式的跳舞的集會,參加者要穿著晚禮服等正裝,整場舞會中很大的一部分由交際舞構成。...
QQ炫舞中的一種遊戲模式。玩家需要和另一名玩家組成搭檔參與遊戲,每局遊戲最多可以有3對搭檔。舞會模式的操作方式和炫舞模式相同 。...
《舞會》是日本作家芥川龍之介創作的短篇小說,發表於1920年1月的《新潮》雜誌上。《舞會》以明治維新時代的鹿鳴館為舞台描寫了一個處於蒙昧狀態的小姐,是怎樣在...
每年的11月,位於法國巴黎協和廣場的克利翁酒店(Hotel de Crillon)總會有一個特殊的夜晚。世界各地的名門貴族、各界名人明星在這晚聚集在一起,舉行一個盛大的舞會。...
世界各地的名門貴族、各界名人明星在這晚聚集在一起,舉行一個盛大的舞會。這就...他闊氣地提出可以自己付錢,歐斐莉雅覺得享受生活不是問題,但不能變成沒品的炫富...
延安舞會又稱延安交際舞是由美國記者艾格妮絲·史沫特萊傳授,史沫特萊於1937年1月底來到延安。延安交際舞作為向封建勢力的挑戰,被逐漸時興起來,陝北黃土地上,寶塔山...
地久天長熱鬧的舞會好孤寂愛我的對象在哪裡滿堂的人潮多擁擠誰能回答我這個老問題熱鬧的舞會無聊極可知我夢想多美麗討厭人對我笑嘻嘻到底誰才能夠讓我動情...
《化裝舞會》記敘了作者童年對他" 一生一定也是有影響"的一件事是:我家的女僕用扮演一個窮人的方式告訴了一個富家子弟(文中的我)一個盤子對食不果腹的窮人是...
1780年,喬治三世為了替以他的皇后莎拉名字命名的產科醫院籌款,舉行了世界上第一個元媛舞會(May Ball),喬治三世在王宮裡接見初次踏入社交季的貴族少女,成為了一個...
《胡偵探傳說之校園舞會連環殺人案》,是《胡偵探傳說》系列中的番外第3部遊戲。也是《胡椒偵探社》系列第1部隱狼篇。該遊戲講述了某市樁語大學的校園舞會發生兩次...
巴黎名媛舞會是一個由法國傳奇女公關、舞會創始人奧菲利(Ophélie Renouard)打造的世界頂尖級名媛舞會。...
所謂百度動漫狂想舞會就是喜歡二次元的人聚集在一起討論的活動相關動漫的知識普及動漫是動畫和漫畫的合稱與縮寫,在其他語言相當少用。隨著現代傳媒技術的發展,動畫(...
《時尚化妝舞會》是一款裝扮小遊戲,遊戲大小為328K。...... 《時尚化妝舞會》是一款裝扮小遊戲,遊戲大小為328K...這個問題就交給你啦!時尚化妝舞會操作指南 編輯 ...
《億萬富翁的舞會:超級富豪如何綁架了世界》是2013年10月1日東方出版社出版的圖書,作者是琳達·麥奎格 (Linda McQuaig)、尼爾·布魯克斯 (Neil Brooks)。...
