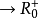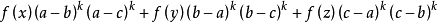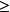舒爾不等式

a,b,c≥0,t∈R⇒a^t(a-b)(a-c)+b^t(b-c)(b-a)+c^t(c-a)(c-b)≥0。

基本介紹

• 中文名：舒爾不等式
• 外文名：Schur's inequality
• 提出：舒爾
• 學科：數學
• 時間：2007年

介紹

a,b,c≥0,t∈R⇒a^t(a-b)(a-c)+b^t(b-c)(b-a)+c^t(c-a)(c-b)≥0

若且唯若a=b=c，或其中兩個數相等而另外一個為零時，等號成立。

特別地，當t為非負偶數時，此不等式對任意實數a,b,c成立。

Schur不等式雖不是聯賽大綱中規定掌握的不等式，但在聯賽不等式證明題中仍能發揮重要作用。

證明

對t=1的證明：

由對稱性，不妨設a≥b≥c，

a(a-b)(a-c)+b(b-c)(b-a)+c(c-a)(c-b)=(a-b)²(a+b-c)+c(c-a)(c-b)≥0，證畢。

對t∈R的證明：

由對稱性，不妨設a≥b≥c，則a^t-b^t+c^t≥0。

a^t(a-b)(a-c)+b^t(b-c)(b-a)+c^t(c-a)(c-b)=a^t(a-b)²+(a-b)(b-c)(a^t-b^t+c^t)+c^t(b-c)²≥0，證畢。

推論

1、a,b,c≥0⇒(a+b-c)(b+c-a)(c+a-b)≤abc。

2、三角形中，a,b,c為角A,B,C所對的三邊⇒cosA+cosB+cosC≤3/2。

3、三角形中，R≥2r。

推廣

假設a、b、c是正的實數。如果（a，b，c）和（x，y，z）是順序的，則以下的不等式成立：

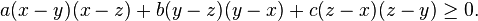
2007年，羅馬尼亞數學家Valentin Vornicu證明了一個更一般的形式：

考慮a，b，c，x，y，zR，其中abc，而且要么xyz，要么zyx。設k ，並設ƒ:R要么是凸函式，要么是單調函式。那么：0

當x = a、y = b、z = c、k = 1、ƒ(m) = m[sup]r[/sup]時，即化為舒爾不等式。

舒爾不等式的如下兩個變形形式在解題中非常有用

變形1：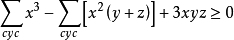

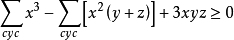
變形2：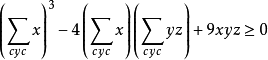

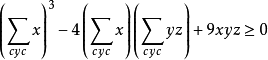
事實上，把①展開即得變形1，因為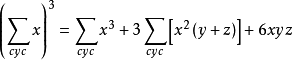,代入變形1，得

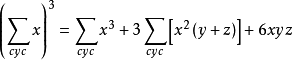
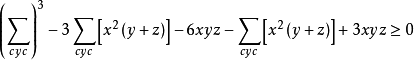
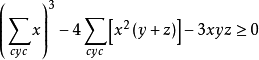
所以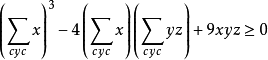

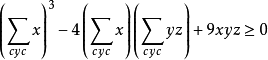
下面引用三個例題來介紹舒爾不等式的用法

例題1：設x，y，z≥0，且x+y+z=1，求證：

0≤yz+zx+xy-2xyz≤7/27

證明：由舒爾不等式的變形2可得;

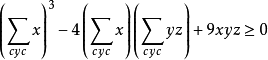
有題設條件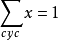可得

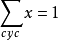
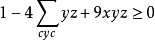
另一方面，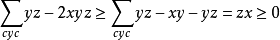

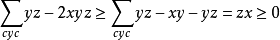
從而命題得證。

例題2

證明：在△ABC中有

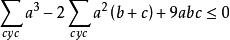
證明：令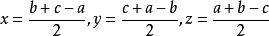,則由舒爾不等式可得

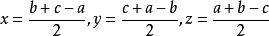
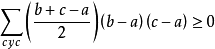
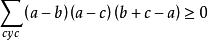
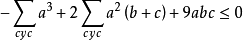
所以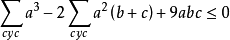

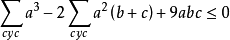
例題3：設x，y，z∈R+，且x+y+z=xyz，求證：

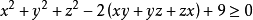
證明：因為x+y+z=xyz, 所以上式等價於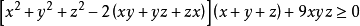

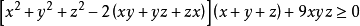
等價於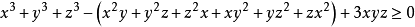

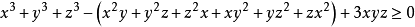
即

這就是舒爾不等式的變形1，故原命題得證！