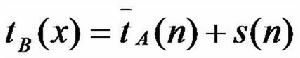舍伍德算法

舍伍德算法是機率算法的一種，該文在比較線性表的順序存儲與鏈式存儲的特點之後，提出了一種較優的數據結構——用數組模擬鍊表。理論上證明了採用舍伍德算法進行查找運算的時間複雜度為0(n^1/2)，並在計算機上給出相應數據的模擬。

基本介紹

• 中文名：舍伍德算法
• 類型：機率算法
• 基本思想：消除或減少問題實例間的差別
• 實現方法：類模版

基本思想

設A是一個確定性算法，當它的輸入實例為x時所需的計算時間記為tA(x)。設Xn是算法A的輸入規模為n的實例的全體，則當問題的輸入規模為n時，算法A所需的平均時間為這顯然不能排除存在x∈Xn使得 tA(x)>>tA(n)的可能性。

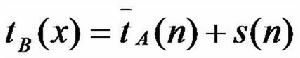
希望獲得一個機率算法B，使得對問題的輸入規模為n的每一個實例均有

這就是舍伍德算法設計的基本思想。當s(n)與tA(n)相比可忽略時，舍伍德算法可獲得很好的平均性能。

舍伍德算法總能求得問題的一個解，且所求得的解總是正確的。當一個確定性算法在最壞情況下的計算複雜性與其在平均情況下的計算複雜性有較大差別時，可以在這個確定算法中引入隨機性將它改造成一個舍伍德算法，消除或減少問題的好壞實例間的這種差別。舍伍德算法精髓不是避免算法的最壞情況行為，而是設法消除這種最壞行為與特定實例之間的關聯性。

2線性表的組織

在現實世界中，線性表的例子枚不勝舉，如一幅撲克牌的點數(2,3,4，…,J，Q，K，A)可構成一個線性表；資料庫表中的記錄也可以構成一個線性表，只不過是該線性表中的數據元索稍複雜一點罷了。正因為線性表如此重要，ANSl和ISO於1998年制定的STL(Standard Template Library)中提供了對線性表的支持。STL的容器是用來放置各種類型的對象，其中每一個容器類就是計算機的一個基本數據結構。STL有以下7個最基本的容器類：向量(Vector)，列表(List)，雙端佇列(Deque)，集合(Set)，多重集合(Multiset)，映像(Map)，多重映像(Multimap)等。

線性表的存儲有兩種方式：順序存儲和鏈式存儲。從空間的角度看，鏈式存儲的存儲密度低，因為它需要存儲附加的指針域的數據。而順序存儲不需要存儲附加信息，因而存儲效率比較高；從時間角度來看，由於順序存儲的邏輯順序與物理順序一致，其存儲可採用其索引號來加以存取，因此是一種隨機存取結構，表中的任意一個結點都可在O(1)的時間內直接存取，但是在表中插入和刪除元索時耍移動大量的元素，該結構適合經常進行查找，很少做插入和刪除運算操作的場台。而鏈式存儲與它恰恰相反，插入和刪除不需要移動元素，只需要修改指針即可，但其查找的時間複雜度卻為O(n)．在STL中容器類中的Vector類採用順序存儲，List類採用鏈式存儲。後面的程式測試就是採用這兩個類來進行的。

有沒有這樣的一個數據結構，即能像鏈式存錯儲結構那樣，插入和刪除不需移動大量元素，在查找時也能像順序存儲結構相似，不會比較報多的數據?況且在一些不包含指針的程式設計語言如Java和VB中，如何實現鏈式存儲結構呢?

3數組實現鍊表

在不包含指針的程式設計語言如VB中，可以採用數組來實現鍊表，實現了“虛假”的指針操作。但就是這種“虛假”指針，恰恰不僅彌補某些指針的某些缺結，還發揮了這種“虛假”指針的優點。採用這種數據結構，拋棄了順序存儲在插入運算中需要移動大量元素的缺點。採用這種數據結構，利用,舍伍德算法進行查找、插入和刪除操作，其效率在傳統的順序存儲和鏈式存儲之間。

在所有的程式設計語言中都有數組，可以利用兩個數組

m_pData和m_pLink來表示所給的含有多個元素的有序集。用m_pData存儲有序鍊表的數據，用m_pLink存儲有序鍊表的數據元索的直接後繼的指針(在數組中的索引號)。m_pLink[O]指向有序鍊表的第一個元素，換句話說，m_pData[m_plink[0]]是有序鍊表中的最小元素。一般來說，如果m_pData[i】是有序鍊表中的第k個元素，則m_pData[m_plink[i]]是有序鍊表中的第k+1個元素。有序鍊表的有序性表現在：對於任意的I≤i≤n，有m_pData[i]≤m_pData[m_plink[i]]。有序鍊表中的最大元素m_pData[k]有m_plink[k]-O(無後繼，指向第零個結點，第零個結點是監視哨)且m_pDaIa[0]為一個大數。

倘若採用順序搜尋的方式在這種有序鍊表中查找指定的元素，每次查找與有序鍊表建立的順序有關，此時採用舍伍德算法可以消除這種聯繫。

利用數組下標的索引性質，可以設計一個隨機化的搜尋算法，以改進搜尋的時間複雜性。該算法的基本思想是隨機選取數組元素若干次，從較接近搜尋元素x的位置開始進行順序查找，而沒有必要從有序鍊表的開始位置進行搜尋，從而較大幅度地提高查找效率。

遺憾的是在STL容器類中的Voctor類採用順序存儲，List類採用鏈式存儲，並沒有這樣的一種數據結構一用數組模擬有序鍊表。模仿標準STL中的類模板的實現，我們編制了一個類模板COrderList，並實現了用舍伍德算法進行查找、插入等算法。

4用類模板實現算法

用類模板實現的算法如下：

template<classType>

boolCOrderlist<Type>：：Search(Type x, int&index)

//搜尋有序鏈襲中的指定元素x、並將其位置放在index變數中

{//mCnrrentNumber為當前有序鍊表中元素的個數，它為類模

//板CorderLisl的數據成員,m為隨機搜尋的次數；

int m=(int)sqrt(double(m_CurmntNumber));

int j;

index=O;

//m_LowBound為當前有序鍊表中最小元素的值．它為類模板

//CorderList的數據成員;

Type max=m_LowBound;

for(int i=l；i<=m，i++}

{j=randl();

//產生一個隨機數j，在數組m_pData[]隨機中找一個值

Type y-m—pDataU]：

If((max<y)&&(y<x))

//找最靠近查找元素x的索引位置Index

{max=y；

index=j；}

}

//從最靠近查找元素x的Index所指向的位置升妯進行順序搜尋

while(m_pData[m_pLink[index]]<x)

index=m_pLink[index]；∥指針後移

return(n_pData[m_pLink[indcx]==x)；//是否找到

}

5程式測試

利用VC6.0編製程序，測試其查找幾十萬個元素用不同的算法所需要的運行時問(機器為賽揚633．記憶體128MB)，結果如表1所示。

表1 數組模擬有序鍊表的查找時間

萬個元素; 算法	10	20	30	40	50
舍伍德算法（s）	1	2	3	4	5
順序查找順序表(s)	4	8	13	18	21
順序查找鏈式表(s)	4	8	12	16	20

總結

採用數組模擬有序鍊表，它本質上是利用兩個數組，一個存儲數據，一個存儲其後繼在數組中的位置，對於查找指定元素，採用舍伍德算法可在0(n)時間內完成，採用順序存儲結構時，若數組元素無序，則只能順序查找，需O(n)時間，若數組元素有序，可進行二分法查找，其時問複雜度雖然降為0(logn)，但卻在進行插入和刪除元素時，需要移動大量元素。與鏈式存儲相比，插入和刪除時雖然都不需要移動元素，但在查找上，其時間性能由0(n)降為O(n)，可見採用數組模擬有序鍊表，並採用舍伍德算法進行查找刪除具有比較高的效率。它不失為一種高效韻數據結構。