基本介紹
- 中文名：舉力線理論
- 外文名：lifting line theory
- ：
- 提出者：普朗特
用一條附著在機翼上的集中渦線（見渦旋）和從機翼順流延伸到無窮遠的尾渦面來代替機翼作用的一種理論；用來計算舉力沿翼展的分布、機翼上的總舉力和由尾渦產生的阻力（稱為誘導阻力）。1907年，從事空氣動力學研究的英國人F.W.蘭徹斯特提出用渦系代替機翼的思想，但未作定量研究。其後德國力學家L.普朗特於1913～1918年提出了舉力線理論。這個理論主要用來計算亞聲速流動中大展弦比直機翼（或小後掠機翼）的舉力和由尾渦引起的阻力，也可推廣用於有後掠的大展弦比機翼。對於大展弦比機翼，每個截面的流動都接近於二維流動。俄國學者Н.Е.儒科夫斯基證明：在不可壓縮的二維流動中， 單位展長機翼上的舉力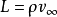
Γ，式中ρ為流體密度；Γ為繞翼型的速度環量；
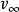為遠前方的流速。圖中虛線表示一個機翼,粗實線AB表示附著渦線,細實線表示尾渦面上的一些渦線。在圖示的機翼上，下翼面的高壓流體繞翼尖向上翼面流動，使翼尖處舉力降為零,沿翼展由中間到翼尖,舉力由大到小,相應的速度環量Γ由最大值降為零，因此，如果用一根附著渦線來代替機翼的作用，渦線必須是變環量的(即Γ 隨翼型位置y而變)。此外,下翼面附近的流體有從中間指向翼尖的分速，上翼面附近情況相反。上下兩股氣流在機翼後緣會合時，將形成一個向下游延伸的渦面(即尾渦面)。利用這樣一個舉力線渦系模型和有關渦旋流動的一些定理和公式可以求出舉力沿翼展的分布和由尾渦引起的阻力。理論證明，有限翼展機翼的舉力隨攻角而變化的斜率比無限翼展的機翼小，斜率與展弦比成反比。尾渦引起的阻力同舉力的平方成正比，同展弦比成反比。舉力線理論在低速飛行器的設計中有廣泛套用。
舉力線理論不適用於小展弦比、大後掠角的機翼。（見舉力面理論）
