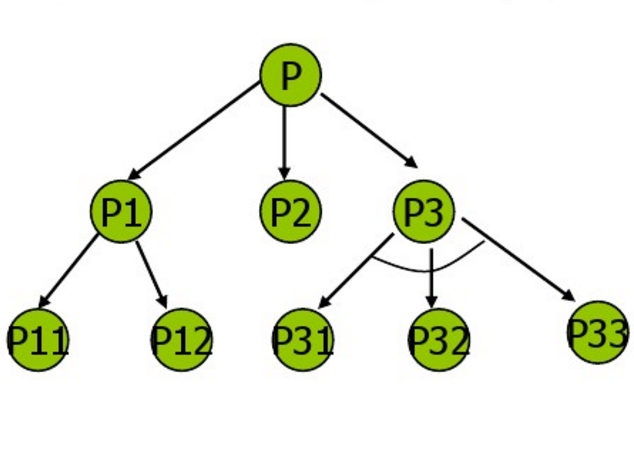
與或圖是由與節點及或節點組成的結構圖。 一般地,我們用一個類似圖的結構來表示把問題歸約為後繼問題的替換集合,這種結構圖叫做問題歸約圖,或叫與或圖。
它是一種系統地將問題分解為互相獨立的小問題,然後分而解決的方法。
基本介紹
- 中文名:與或圖
- 外文名:And-Or graph
相關術語,一般搜尋過程,廣度優先搜尋,深度優先搜尋,有序搜尋,
相關術語
終葉節點:對應於原問題的本原節點。
或節點:只要解決某個問題就可解決其父輩問題的節點集合,如(M,N,H)。
與節點:只有解決所有子問題,才能解決其父輩問題的節點集合,如(B,C)和(D,E,F)各個結點之間用一端小圓弧連線標記。
或節點:只要解決某個問題就可解決其父輩問題的節點集合,如(M,N,H)。
與節點:只有解決所有子問題,才能解決其父輩問題的節點集合,如(B,C)和(D,E,F)各個結點之間用一端小圓弧連線標記。
一般搜尋過程
(1)把原始問題作為初始節點S0,並把它作為當前節點;
(2)套用分解或等價變換操作對當前節點進行擴展;
(3)為每個子節點設定指向父節點的指針;
(4)選擇合適的子節點作為當前節點,反覆執行第(2)步和第(3)步,在此期間需要多次調用可解標記過程或不可解標記過程,直到初始節點被標記為可解節點或不可解節點為止。
廣度優先搜尋
與狀態空間的廣度優先搜尋類似,搜尋原則:先產生的節點先擴展。只是在搜尋過程中需要多次調用可解標記過程或不可解標記過程。
設有如下圖所示的與/或樹,節點按圖中所標註的順序號進行擴展,其中標有t1、t2、t3、t4的節點是終止節點,A、 B 為不可解的端節點。
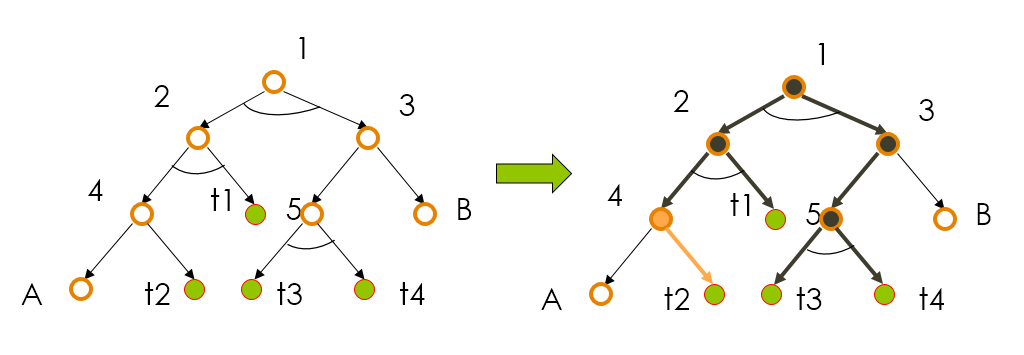
深度優先搜尋
Open表中節點的排列順序:剛生成的節點放在Open表的首部,為每個子節點配置指向父節點的指針,也可以帶有深度限制dm。
有序搜尋
1. 最優解樹: 代價最小的那棵解樹。
2.節點的代價
(1)若n為終止節點,h(n)=0。
(2)若n為或節點,且子節點為n1,n2,…,nk, h(n)= min {c(n,ni)+ h(ni)} (1≤i≤k)
(3)若n為與節點,且子節點為n1,n2,…,nk, 和代價法: h(n)= ∑((c(n,ni)+ h(ni)) =1,2,……,k
最大代價法: h(n)= max{c(n,ni)+h(ni)} (1≤i≤k)
(4)若n是端節點,但又不是終止節點,則n不可擴展, h(n)= ∞
3. 解樹的代價:初始節點S0的代價
有序搜尋過程:
圖搜尋由兩個過程組成: 自頂向下,圖生成過程,擴展節點,從希望樹中選擇一個節點擴展 自底向上,計算代價過程,修正代價估值,重新選擇希望樹。