波函式是量子力學描寫微觀系統狀態 (又稱量子態或態) 的函式。是量子力學基本原理之一,也是量子力學中最基本最重要的量。在經典力學中,用質點的位置和動量(或速度) 來描寫巨觀質點的運動狀態,當坐標和動量確定之後,質點的其他力學量,如能量等也就隨之確定了。
自旋波函式是描述原子在自旋時系統狀態的波函式。
基本介紹
- 中文名:自旋波函式
- 外文名:Spin wave function
- 領域:物理
- 學科:量子力學
- 性質:波函式
- 特點:描述原子自旋狀態
概念
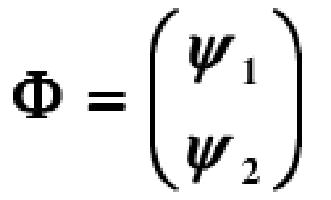
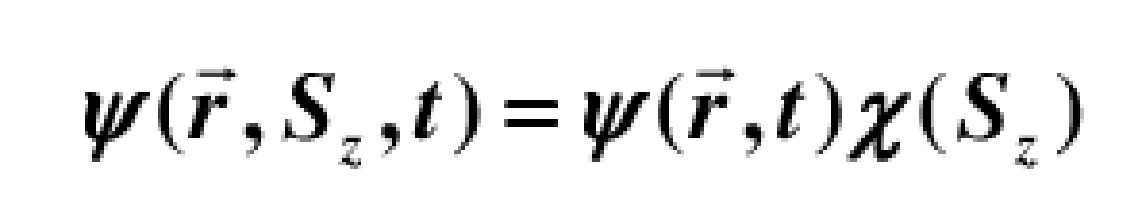
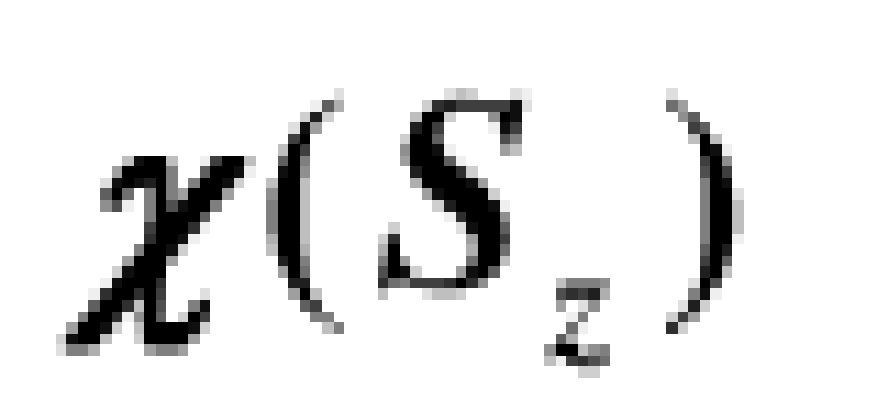
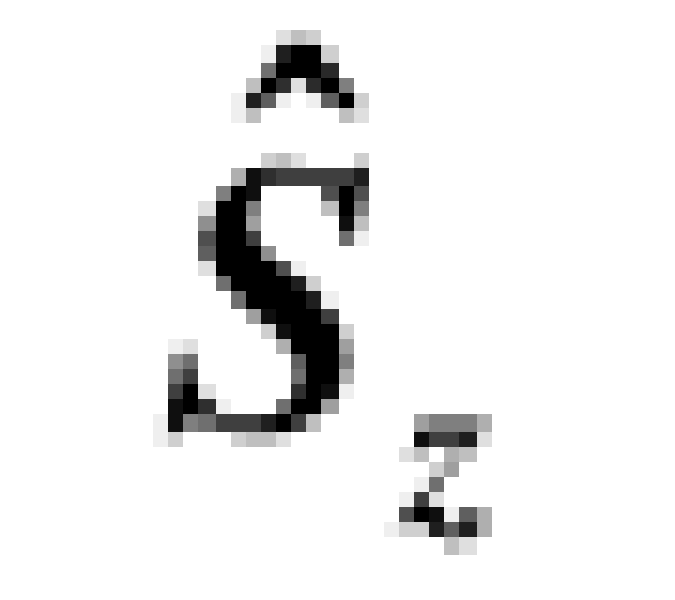
量子力學
自旋
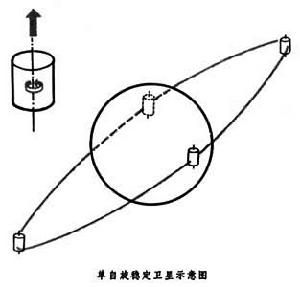
波函式是量子力學描寫微觀系統狀態 (又稱量子態或態) 的函式。是量子力學基本原理之一,也是量子力學中最基本最重要的量。在經典力學中,用質點的位置和動量(或速度) 來描寫巨觀質點的運動狀態,當坐標和動量確定之後,質點的其他力學量,如能量等也就隨之確定了。
自旋波函式是描述原子在自旋時系統狀態的波函式。
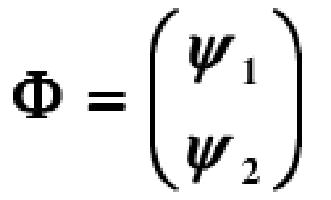
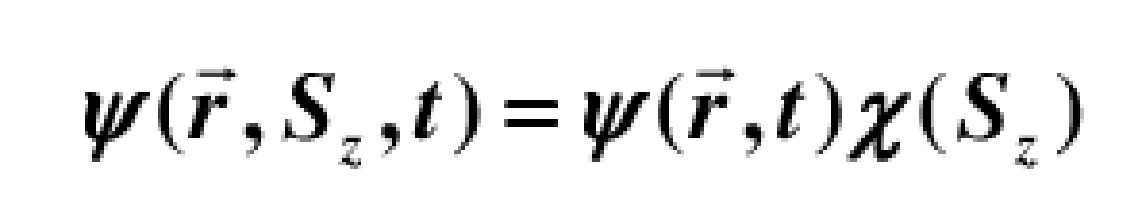
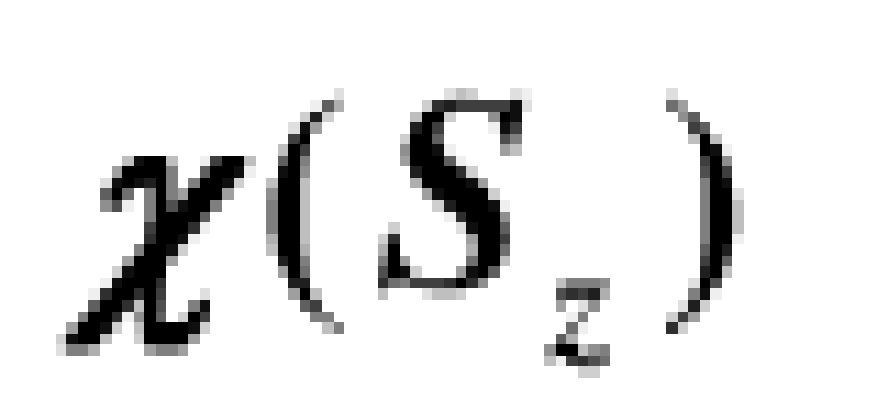

波函式是量子力學描寫微觀系統狀態 (又稱量子態或態) 的函式。是量子力學基本原理之一,也是量子力學中最基本最重要的量。在經典力學中,用質點的位置和動量(或速度) 來描寫巨觀質點的運動狀態,當坐標和動量確定之後,質點的其他...
在定域的相對論性量子場論(見量子統計法)中,由微觀因果性或能量子定性要求,可以證明自旋量子數為整數的全同粒子系統的波函式必須是對稱的;自旋量子數為半整數的全同粒子系統的波函式必須是反對稱的。由此推知,自旋量子數為整數的...
本項目在相對論平均場模型的基礎上首先利用重整化群方法進一步研究了贗自旋對稱性的同位旋不對稱性。研究結果表明:贗自旋能級對稱性的同位旋不對稱性主要是因為ρ場對動力學項施加影響而產生的,而ρ場和庫侖場對於贗自旋波函式對稱性的...
s與l相當,稱s為自旋量子數。(l 叫軌道量子數或角量子數)。自旋算符的本徵波函式 本徵:當我們僅研究自旋性質時,系統的空間部分波函式可以視為常數,選擇 表象,則算符的兩個本徵態為:一般態:當體系自旋處在一般態 時,由...
常稱為自旋磁量子數。常用記號與β分別代表與的狀態。於是包括自旋狀態的波函式用四個量子數、l、、作為標記,則波函式為 (14)可以把軌道角動量與自旋合成總角動量,在封閉系統中總角動量是守恆量。以(有時用)表示總角動量,則有...
這個悖論的唯一解是該波函式的值為零:比如在上面的例子中假如兩個粒子的位置波函式一致的話,那么它們的自旋波函式必須是反對稱的,也就是說它們的自旋必須是相反的。該原理說明,兩個電子或者兩個任何其他種類的費米子,都不可能占據...
§6.2分波法 §6.3Born近似 習題 第7章自旋與角動量 §7.1電子自旋 §7.2自旋波函式自旋算符Pauli方程 §7.3簡單Zeeman效應 §7.4磁共振 §7.5兩個角動量的耦合C-G係數 §7.6光譜的精細結構複雜Zeeman效應 §7.7自旋單...
4.4 電子自旋 176 4.4.1 施特恩-格拉赫實驗 176 4.4.2 鈉原子光譜線的精細結構 179 4.4.3 電子自旋假設 180 4.4.4 自旋波函式 181 4.4.5 自旋算符 182 4.4.6 自旋在任意方向投影的波函式 185 4.4.7 泡利方程 186...
使得困難的三體問題變得容易處理;與通常的兩體問題不同的是,重輕子的自旋所引起的效應並未略去,因而本文結果中計入了由重輕子的自旋所導至的三體效應,它具體表現為體系的自旋波函式的結構之中,並在實驗觀察中表現為與兩粒子體系不...
5.6 低能散射——分波法 5.7 高能散射-Born近似 第6章 自旋與全同粒子 6.1 電子的自旋算符和自旋波函式 6.2 兩個角動量的耦合 6.3 光譜的精細結構 6.4 全同粒子的特徵和波函式Pauli原理 6.5 兩個電子的自旋函式氦原子 ...
量子力學所用概念:絕熱近似,相應原理,自由粒子,哈密頓,希爾伯特空間,等同粒子,矩陣力學,普朗克常數,算符,量子,量子化,量子糾纏(quantum entanglement),量子諧振子,量子數,量子隧道,迪拉克方程,自旋波函式,波-粒雙重性,零點...
2.3 電子自旋 (42)2.3.1 自旋波函式、空間波函式和全波函式 (42)2.3.2 全同粒子和斯萊特行列式 (42)2.3.3 電子自旋與物質的磁性 (43)2.4 原子光譜與原子光譜項 (45)2.4.1 原子光譜精細結構 (45)2.4.2 ...
第七章 自旋 §7.1 電子自旋 §7.2 電子的總角動量 §7.3 鹼金屬光譜的精細結構 §7.4 粒子在電磁場中的運動 §7.5 塞曼效應 §7.6 磁共振 §7.7 兩個角動量的耦合 §7.8 二電子體系的自旋波函式 習題 第八章...
4.2.1全同性原理和波函式的交換對稱性(143)4.2.2泡利不相容原理(145)4.2.3兩個電子的自旋波函式(145)4.2.4氦原子的波函式與交換效應(147)4.3多電子原子的電子組態和殼層結構(151)4.3.1多電子原子的中心力場近似和...
§1—8 電子自旋 1.電子自旋問題的提出 2.自旋波函式和自旋軌道 3.泡利原理與多電子波函式 §1—9 原子核外電子排布與元素周期律 1.原子核外電子排布與元素周期律 2.離子的電子層結構 §1—10 多電子原子的量子數和原子光譜...
強子及其波函式 常見的強子分重子和介子兩大類,其中重子是由三個夸克或三個反夸克組成,介子是由一個夸克和一個反夸克組成。強子的味取決於構成強子的夸克的味。且有:強子波函式=時空波函式×味道波函式×自旋波函式×顏色波函式。...
五、電子的自旋與自旋波函式 1 施登?蓋拉赫(Stern?Gerlach)實驗 2 電子自旋假設 3 自旋與自旋在磁場方向分量的表達式 4 自旋軌道與自旋波函式 六、基態原子核外電子排布的原則 1 泡利(Pauli)不相容原理 2 能量最低原理 3 洪德(...
