自動化理論-圖靈機

英國數學家A.M.圖靈提出的一種抽象計算模型，用來精確定義可計算函式。

圖靈機由一個控制器、一條可無限延伸的帶子和一個在帶子上左右移動的讀寫頭組成。這種機器有一條無限長的紙帶，紙帶分成了一個一個的小方格，而每個方格有不同的顏色。有一個機器頭在紙帶上不斷移來移去。機器頭有一組內部狀態，還有一些固定的程式。在每個時刻，機器頭都要從當前紙帶上讀入一個方格信息，然後結合自己的內部狀態查找程式表，根據程式輸出信息到紙帶方格上，並轉換自己的內部狀態，然後進行移動。

圖靈機不僅可以衡量可計算性，而且可以用於衡量問題的計算複雜性。另一方面，圖靈機還是現代電子計算機的理論模型，算法設計和程式設計方法等都與圖靈機理論方法有著密切關係

基本介紹

• 中文名：圖靈機
• 外文名：Turing machine
• 核心要素：有限狀態控制器
• 創始人：圖靈
• 主要用途：用於衡量一類問題是否可判定
• 組成：輸入帶、控制裝置和連線讀寫頭

概述

圖靈機是由英國數學家圖靈（A.M.Turing，1912~1954）在1936年提出的一種計算模型。同遞歸函式和λ-演算相比較，圖靈機的結構和運行同希爾伯特提出的形式系統更為接近，只不過圖靈機並不是（入希爾伯特所希望的那樣）用於判定命題的正確性，而是用於衡量一類問題是否可判定，也就是說，圖靈機同遞歸函式和λ-演算一樣，是衡量問題的可計算性的計算模型。

基本概念

從機械裝置的角度來說，圖靈機由一條可以（向右）無限延伸的輸入帶，一個有限狀態控制裝置和一個連線控制器與輸入帶的讀寫頭組成

如圖。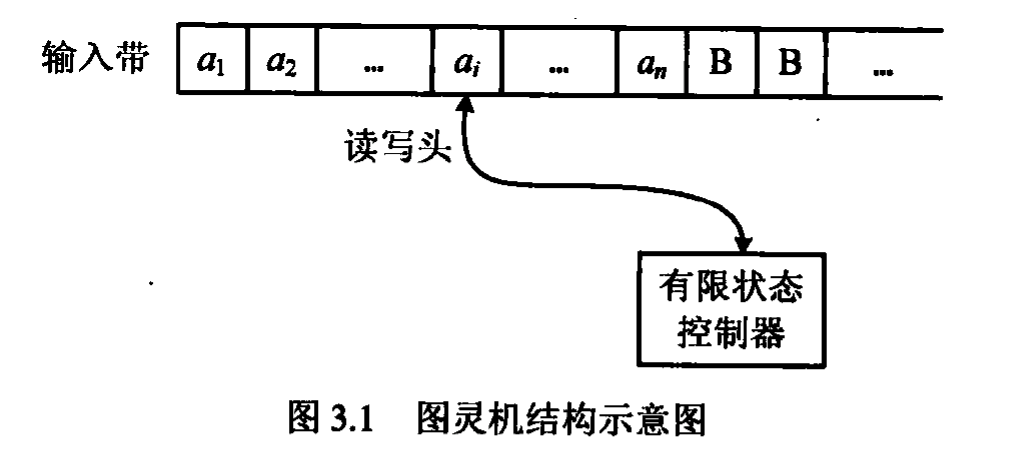

有限狀態控制器中的狀態轉換及動作規則是圖靈機的核心要素。當讀寫頭掃描輸入帶上的一個格（即讀到一個帶符號）時，結合圖靈機的當前狀態，在有限狀態控制器（根據狀態轉換及動作控制規則）的控制下，圖靈機執行下列三項工作：

（1）進行狀態轉換；

（2）讀寫頭在帶上的當前格寫上新的字元；

（3）決定讀寫頭向左還是向右移動一格。

對於帶上的一個輸入字元串，圖靈機從初始狀態和帶上最左邊的字元開始，通過連續不斷地掃描和執行相關的動作，如果在某個時刻進入終止狀態，圖靈機就接受輸入串。被一個圖靈機所接受的全部字元組成的集合，就是圖靈機所接受的語言。

形式定義

圖靈機是一個七元組

M=(Q,Ε,Γ,δ,q₀,B,F)

其中，Q是有限狀態集，Ε是輸入字母表，Γ是帶符號集，δ：是動作函式（L表示讀寫頭向左移動一格，R表示讀寫頭向右移動一格），q₀（q₀∈Q）是初始狀態，B（B∈Γ）表示空白符，F（F⊆Q）是終止狀態集。

可以給出接受語言L1的圖靈機的形式定義如下圖

一個圖靈機M識別一格輸入串w，可能會遇到下面三種情況：

1. 進入終止狀態，即在瞬像推導過程中遇到一格瞬像ID：x₁...x_i-1x_i...x_n其中q∈F。這時圖靈機M停機，並接受輸入串w。
   
2. 未進入終止狀態，但推導過程停止。即瞬像推導過程中遇到一個瞬像ID:x₁...x_i-1x_i...x_n使得q∉F，但δ（q,x_i）無定義。這時圖靈機M停機，但不接受w。
   
3. 陷入死循環，即在瞬像推導過程中，一直沒有進入終止狀態，而δ又一直有定義。這時圖靈機M（對輸入串w）永不停機。
   

圖靈機用於計算整函式

除了接受語言以外圖靈機還具有函式計算功能。最顯見的是對整函式的計算，即實現對以非負整數為自變數且函式值也是非負整數的函式的計算。通常的，可以用連續i個0來表示整數I。如果一個函式有k個自變數i_1，i₂...i_k,則表示為0ⁱ¹10ⁱ²1...10^ik，各個0字元塊之間的1作為分隔設定。

用於計算整函式的圖靈機不必設定終止狀態。

圖靈機的構造技巧

要構造一個圖靈機實現一定的功能，不是一件輕而易舉的事情，原因就在於圖靈機的每一步動作都非常的簡單，除了內部的狀態轉換之外，對讀寫帶的操作最多的就是修改一格的字元，以及讀寫頭向左或向右移動一格。當接受的語言或計算的函式比較複雜時，要構造出具有相應功能的圖靈機就更不容易。這時就需要採用一些輔助技巧，其中一些技巧在電子計算機的程式設計中都得到沿用。

控制器儲存信息

有時，可以通過用控制器儲存一些關鍵信息來實現某些功能。所謂控制器儲存信息，就是把圖靈機的狀態設定為一個二元組（也可以是一個多元組），前一個客體仍用於表示傳統意義下的狀態，後一個客體則用於儲存有關的信息。

移位

運用控制器儲存信息的技巧，可以使得圖靈機實現移位功能，即把讀寫帶上的全部非空白符整體向左或向右移動若干格，如右圖。

讀寫帶設定為多道軌線

把讀寫帶設定為多道軌線對於實現圖靈機的某些計算功能可以帶來很大的方便。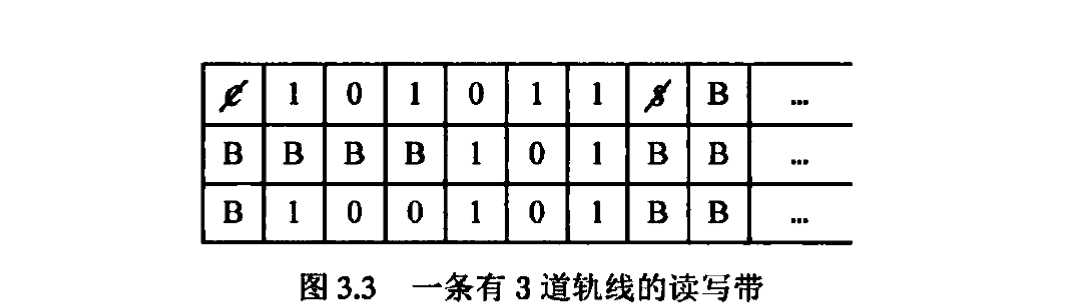

子程式

即可以設計一個圖靈機作為另一個圖靈機的子圖靈機。需要注意的是要做好主圖靈機和子圖靈機之間的銜接，即主圖靈機對子已累計的調用以及子圖靈機完成工作後對主圖靈機的返回，這些可以通過狀態設定來實現。

變形圖靈機

圖靈機可以有很多的變形模型，這些變形模型接受語言或計算函式的能力同基本模型是等價的，然而用他們對某些語言進行識別，或對某些函式進行計算，可能比原型圖靈機更方便。

1. 雙向無限帶圖靈機，
   讀寫向左右兩個方向無限延伸。
   
2. 多帶圖靈機，
   有k（k>1）條讀寫帶和k個讀寫頭，每條讀寫帶向兩個方向無限延伸，並且帶上都有一個讀寫頭痛有限狀態控制器相連線。
   
3. 不確定的圖靈機，
   一種狀態下讀到一個字元，產生的動作可能有多種。
   
4. 脫線圖靈機，
   有一條專用的輸入帶，用於存放輸入串，對這條帶上的字元只能讀，不能寫，另用其他讀寫帶進行工作
   

通用圖靈機

已經證明，存在一個圖靈機U,它可以模擬任何其他的圖靈機T,這樣的U稱為通用圖靈機。U的帶子上記錄著被模擬機器T的指令描述，也記錄著T的問題數據。在工作過程中，U根據輸入帶上記錄的T的指令，模擬T的動作，處理問題的數據。這樣，U可以模擬任何計算過程。

就圖靈機是現代電子計算機的理論模型而言，通用圖靈機的概念有著非常重要的意義。如果沒有圖靈機的概念，一個圖靈機只能實現一種特定的計算，不同的計算功能用不同的圖靈機來實現，然後把不同功能的圖靈機轉化成不同功能的電子計算機。這樣，當我們要解決一個包含多種計算的複雜問題是，就要根據計算流程不斷更換電子計算機。電子計算機的高速運算的優點就會被這種頻繁更換設備的做法抵消。也就是說，現代電子計算機的總體設計思路是從通用圖靈機的概念衍生出來的，而程式設計的概念則是由實現具體計算的圖靈機衍生出來的。

圖靈機停機問題的不可判定性

根據邱奇圖靈論題，圖靈機可以用作衡量各種問題是否可計算（是否可判定）的工具。然而，同圖靈機本身相關的許多問題有事不可判定的。其中圖靈機停機問題就是最有代表性的一個不可判定的問題。這個問題同哥德爾不完全性定理一起，成為哲學家們闡述辯證唯物主義認識論的科學依據。

定理：不存在這樣一個算法，對任意一個圖靈機M=(Q,Ε,Γ,δ,q₀,B,F)和任意一個輸入串x∈E*，這個算法都能判定M對x是否停機。

解釋一下就是圖靈機根據機器的程式處理初始格局。有的初始格局可能導致停機，有的則導致無限的格局序列。停機問題是：是否存在一個算法，對於任意給定的圖靈機都能判定任意的初始格局是否會導致停機。而這樣的算法是不存在的，即停機問題是不可判定的。

停機問題是研究許多不可判定問題的基礎，人們往往把一個問題的判定歸結為停機問題：“如果問題 A可判定，則停機問題可判定。”從而證明問題 A的不可判定性。停機問題有多種不同的敘述方式和證明方法，它們分別適用於具有不同特徵的問題。