臨界群

臨界群（Critical group ）是用以反映臨界點性態的有關水平集的相對同調群。

基本介紹

• 中文名：臨界群
• 外文名：Critical group 
• 作用：反映臨界點性態
• 適用範圍：數理科學

簡介

臨界群是用以反映臨界點性態的有關水平集的相對同調群。

設X是希爾伯特流形，f∈C¹(X,R)，x₀是f的孤立臨界點，f(x₀)=c。取x₀的鄰域U使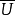中僅含f的惟一臨界點x₀，記

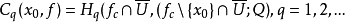其中H_q為q階奇異（相對）同調群，Q為係數群，則C_q(x₀,f)稱為f的孤立臨界點x₀的q階臨界群。

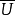
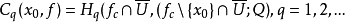
推廣

若f∈C²(X,R)，x₀是f的非退化臨界點，其莫爾斯指數為j，則有

一般地，設a<b為f的兩個正則值，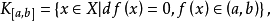

並設X完備，f滿足(P.S)條件，這時同調群H_q(f_b,f_a;Q)稱為K_[a,b]的q階臨界群。

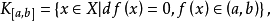
泛函的臨界點

泛函的臨界點是泛函的梯度為零的點。

關於泛函的臨界點的研究成果形成了頗為系統的臨界點理論，它為研究非線性梯度運算元方程的解提供了理論工具。由於一些散度型微分方程的解恰是相應的積分泛函（亦稱變分泛函）的臨界點，因此，用臨界點理論研究非線性方程的方法被稱為非線性分析的變分方法。