基本介紹
- 中文名:臨界力
- 套用領域:機械,建築
- 計算:3.14平方乘以E和I與L的平方之比
- 影響因素:壓桿的材料,截面積大小,長度
計算公式
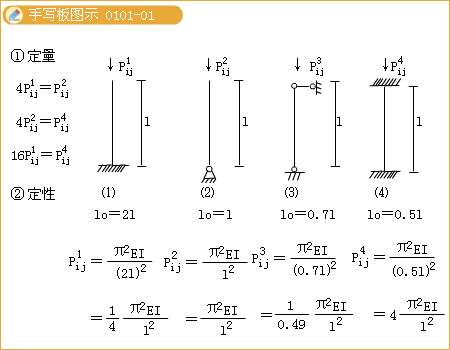 臨界力Pij的大小與支承條件的關係圖
臨界力Pij的大小與支承條件的關係圖案例解析
臨界力和歐拉公式
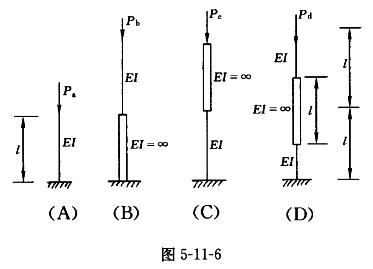
壓桿的臨界應力
材 料 | |||
A3鋼 | 304 | 1.12 | 102 |
優質碳鋼 | 461 | 2.568 | 95 |
鑄 鐵 | 332.2 | 1.454 | 70 |
木 材 | 28.7 | 0.190 | 80 |

 臨界力Pij的大小與支承條件的關係圖
臨界力Pij的大小與支承條件的關係圖
材 料 | |||
A3鋼 | 304 | 1.12 | 102 |
優質碳鋼 | 461 | 2.568 | 95 |
鑄 鐵 | 332.2 | 1.454 | 70 |
木 材 | 28.7 | 0.190 | 80 |
,承受軸向應力(壓應力)P,當軸向應力P增加到一定程度P'(小於許壓應力)時,壓桿的直線平衡狀態開始失去穩定,產生彎曲變形,這個力具有臨界的性質,因此稱為臨界力。...
壓桿處於臨界平衡狀態時(F=Fcr ),其橫截面上的正應力稱為臨界應力。不同的壓桿一般具有不同的臨界應力,臨界應力的大小與壓桿的長度、截面的形狀和尺寸、兩端的...
臨界分切應力(Critical resolved shear stress)簡稱CRSS,又稱Schmid定律,是指把滑移系開動所需要的最小分切應力稱為臨界分切應力。在滑移、孿生變形中有一定的臨界...
火電廠超超臨界機組和超臨界機組指的是鍋爐內工質的參數達到或超過臨界壓力以上的機組。鍋爐內的工質都是水,水的臨界壓力是22.129MPa,臨界溫度是374.15℃ ;在...
斷裂應力,為纖維截面積上能承受的最大拉伸力,這是各種材料通用的表示材料相對強度的指標,一般用σ表示,標準單位為N/m2(帕,Pa),但常用N/mm2(兆帕,MPa)表示。...
也有學者發現在一些合金中存在一個臨界應力值,當外加應力低於此應力值時,其對氧化膜的生長几乎沒有影響,而當其高於此值時會促進氧化膜的生長,這可能是與氧化膜...
8.4 非細長壓桿的臨界應力8.5 臨界應力總圖8.6 安全因數與穩定性分析8.7 提高壓桿穩定性的措施習題第9章 點與剛體的運動分析9.1 點的運動分析...
6.8彎曲與扭轉的組合受力思考題習題第7章壓桿穩定7.1壓桿穩定的概念7.2細長壓桿的臨界力7.2.1兩端鉸支細長壓桿的臨界力7.2.2下端固定、上端自由細長壓桿...
15.2 壓桿臨界力的歐拉公式15.2.1 兩端鉸支壓桿的臨界力15.2.2 桿端約束不同的壓桿臨界力15.3 歐拉公式的適用範圍 臨界應力總圖15.3.1 臨界應力柔度(...
屈服極限 ,常用符號σs,是材料屈服的臨界應力值。(1)對於屈服現象明顯的材料,屈服強度就是屈服點的應力(屈服值);(2)對於屈服現象不明顯的材料,與應力-應變的...
岩石既可發生穩定蠕變也可發生不穩定蠕變,這取決於岩石應力的大小。超過某一臨界應力時,蠕變向不穩定蠕變發展。小於此臨界應力時,蠕變按穩定蠕變發展。通常稱此臨界...
群速度概念,將許多單擺上端串聯且均勻分布在一緊張水平弦線上以演示群速度;指出氣流超聲速地經管道最小截面時的壓力(臨界壓力)(1895);引進湍流中有關應力的概念(...
這一狀態所對應的外載荷稱為臨界載荷,其大小稱為臨界值,板殼內的相應應力稱為臨界應力,記為σcr 。失穩臨界應力值與結構的構造形式、邊界條件、材料性能、載荷...
應以相應於該臨界應力的切線模量 來代替,用彈性狀態時求臨界載荷的同樣方法,導出兩端鉸支軸向壓桿塑性狀態的臨界載荷為稱 為切線模量臨界載荷。上...
