簡介
材料在力的作用下將發生變形。通常把滿足虎克
定律規定的區域稱彈性變形區,把不滿足虎克定律和過程不可逆的區域稱塑性變形區。由彈性變形區進入塑性變形區稱之為屈服。其轉折點稱為屈服點。該點處的應力稱為屈服應力或臨界應力。
有些材料的屈服現象並不明顯,為了便於比較,就人為規定應力—應變偏離直線關係達某值(例如,通常規定為0.2%的永久變形)時的點為屈服點,該處的應力為臨界應力。應該指出,塑性材料的臨界應力和載入速度,工作溫度等有非常明顯的相關性。
臨界應力就是應力的極限值。當材料在外力作用下不能產生位移時,它的幾何形狀和尺寸將發生變化,這種形變稱為應變(Strain)。
材料發生形變時內部產生了大小相等但方向相反的反作用力抵抗外力,定義單位面積上的這種反作用力為應力(Sress)。
按照應力和應變的方向關係,可以將應力分為正應力和切應力,正應力的方向與應變方向平行,而切應力的方向與應變垂直。按照載荷(Load)作用的形式不同,應力又可以分為拉伸壓縮應力、彎曲應力和扭轉應力。
單相多晶體材料屈服臨界分切應力估算
眾所周知,臨界分切應力是晶體材料滑移系開動所需的最小切應力,其數值大小在一定程度上體現了材料抵抗塑性變形的能力。確定晶體材料臨界分切應力的主要方法是通過製備單晶試樣並進行壓縮試驗後分析而得。常見的單晶製備方法有高溫梯度定向凝固法、水平Bridgman法以及Czochralski法。然而受到單晶製備條件的限制,一些特定成分或者特殊相態的金屬與合金單晶並不容易製備叫。通常這些材料更多的是以多晶體狀態存在,因此測定這類材料的臨界分切應力存在一定的困難。與單晶體的臨界分切應力不同,多晶體材料中滑移系開動所需的最小分切應力不僅只與材料的固溶原子、第二相粒子、位錯密度和試驗溫度等因素有關,由Hall-Petch關係可知,晶粒尺寸也對多晶體材料屈服臨界分切應力產生影響,晶粒越細小屈服切應力越大。多晶體材料屈服臨界分切應力不僅能夠反映材料本身的強度,在己知多晶體材料巨觀織構的前提下,還可以利用屈服臨界分切應力預判其力學性能各向異性規律。因此,研究探討直接測算多晶體材料的屈服臨界分切應力,不但為評估多晶體工程材料的強度提供一種便捷有效的方法,而且對深入了解多晶體材料力學性能各向異性特徵有著重要的意義。
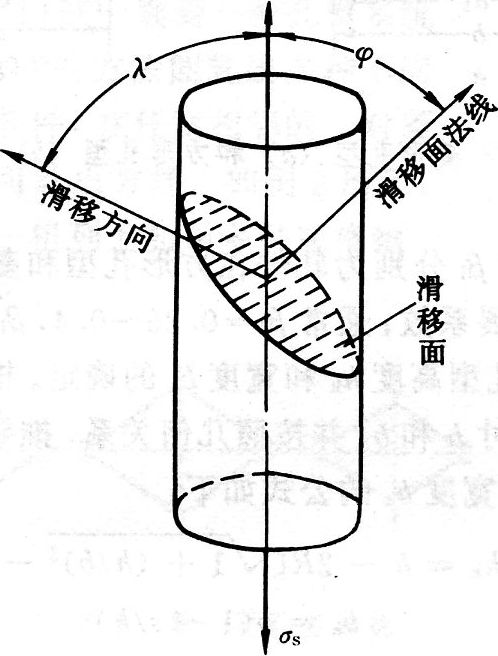
鋼鐵材料作為被套用最廣的多晶體材料,迄今卻鮮有文獻詳細記載不同組織、成分鋼材的屈服臨界分切應力,因此選擇工程鋼材作為研究對象。通常鋼鐵材料的生產加工過程中都存在變形與相變過程,這造成鋼材存在一定量的織構。Schmid定律給出了外載荷、晶體取向與臨界分切應力三者的關係。從而可以依照Schmid定律,結合多晶體材料的實際巨觀織構與力學實驗結果,通過選擇合理的晶體學塑性變形模型對多晶體材料屈服臨界分切應力進行估算。
臨界分切應力估算過程
利用所建模型估算SPHC熱軋板與X100管線鋼臨界分切應力的結果符合相關的金屬學原理,估算值在理論範圍內。此外,材料屈服臨界分切應力是材料的秉性,通常不會表現出各向異性。利用不同取向的實驗數據對所計算結果進行驗證,計算出的各取向屈服臨界分切應力幾乎相同,其標準差不超過0. 1,這也體現了多晶體材料屈服臨界分切應力計算模型的自洽性與可靠性。
由於晶體學織構的存在,多晶體材料屈服強度可能會存在一定程度的各向異性。因此可以利用多晶體屈服臨界分切應力計算模型,結合多晶體材料的巨觀織構,對多晶體材料屈服強度各向異性的規律進行預測。在己知多晶體材料屈服強度的前提下,可以利用該模型估算多晶體材料巨觀屈服時彈性變形與塑性變形晶粒各自的體積分數。此外,還能通過計算出同種多晶體材料不同晶粒尺寸與織構狀態下的屈服臨界分切應力。
然而,該計算模型仍然存在一定的局限性,即僅適用於估算單相多晶體材料的臨界分切應力。當多晶體材料為多相組織,分別確定各相組織的ODFs時,該模型仍存在一定的困難,僅依靠獲得各相體積分數不足以對材料各相的臨界分切應力進行估算。另外,由於該計算模型忽略了彈性變形晶粒與塑性變形晶粒之間的作用,估算值可能與實際臨界分切應力存在少量的偏差。這是由於晶粒的塑性變形量受到其周圍晶粒彈性變形量的制約,滑移系開動晶粒中的位錯可能會在相鄰彈性變形晶粒的晶界處塞積,間接提高了材料的位錯密度,從而提高了屈服臨界分切應力。因此利用計算模型估算出的多晶體材料屈服臨界分切應力數值上可能略微大於實際臨界分切應力。
總結
分析多晶體材料在變形初期晶粒的彈性變形與塑性變形行為。當應變數很小時,在多晶體塑性變形的Sachs模型基礎上,通過利用Schmid定律區分出多晶體材料在巨觀屈服狀態下塑性變形晶粒與彈性變形晶粒,建立了多晶體材料屈服臨界分切應力的計算模型,且計算模型合理可行。