膠結指數

膠結指數是用來計算岩石孔隙結構的一個指數，由於裂縫和孔洞的存在，導致了儲層的非均質性，造成孔隙膠結指數m等岩電參數的改變。如水泥膠結指數（ cement bond index）是指油田固井質量檢查指數。

基本介紹

• 中文名：膠結指數
• 外文名：cementation index
• 描述：岩石孔隙度計算
• 用途：油田固井質量檢查的一個指數
• 學科：地球物理勘探

概念

含水岩石的電阻率與孔隙度之間的關係可以用阿爾奇公式一般表示為F=a/9ψm，式中m稱為膠結指數，ψ為孔隙度，F為地層因數。實際上m值與岩石的孔隙結構有關。

孔隙儲層膠結指數的確定方法及影響因素

含有裂縫和孔洞的碎屑岩儲層、碳酸鹽岩儲層、火成岩儲層以及變質岩儲層都是複雜孔隙儲層。作為複雜地層的測井解釋模型研究，它是基於純砂岩、泥質砂岩基礎上發展起來的，其發展基礎是阿爾奇公式，在運用阿爾奇公式進行含水飽和度的計算時，複雜儲層的非均質性對於參數的要求很高，這些參數隨地區的地質特徵而變化，甚至在所研究的各個儲層有不同的取值範圍。許多學者對於孔隙度膠結指數m和飽和度指數等岩電參數做了研究與計算。對於孔隙度膠結指數m的計算主要有兩條方向：一是通過岩電實驗進行統計；二是基於孔隙模型進行推導。

基於岩電實驗的膠結指數值研究

許多學者通過岩電實驗對孔隙膠結指數m進行了研究和計算。針對塔河油田通過遞歸分析得到了膠結指數m。針對鄂爾多斯盆地中部氣田基質低孔隙裂縫性碳酸鹽岩儲集層，通過高溫高壓、常溫常壓岩—電實驗進行研究分析，結果表明，該地區儲集層對水溶液體積增量的敏感性是非阿爾奇特性的主要原因，孔隙度與孔隙結構指數m呈函式動態變化關係，不完全服從常數性m值關係式。針對類似川東北地區以溶孔型、裂縫—溶孔型為主的中低孔隙度的海相碳酸鹽岩儲集層進行岩電實驗，因該地區儲集層具有橫向變化大、縱向各層組孔隙結構各不相同的特徵，僅以層組來區分m、n值具有一定局限性，必須在按層組統計的基礎上，再利用不同孔隙度區間來進一步回歸m值、n值,由岩電實驗數據回歸得到不同層段、不同孔隙類型的m值。對普光地區縫洞性儲層岩電參數的影響因素進行了分析，分別討論了地層水礦化度、泥質含量、溫度和孔洞縫發育程度對孔隙結構指數m的影響，得出的地層條件下m值的變化規律為：隨地層水礦化度的增大，m值呈增大趨勢；隨溫度和孔隙度的增大，m值增大。此外，針對富台潛山和蘇德爾特油田達特群潛山油藏複雜儲層，針對建南氣田碳酸鹽岩儲層，以及相關學者分別對各自地區儲層參數進行了分析研究和計算。

（1）岩電實驗法m值的比較

根據塔河油田、川東北地區、普光地區和建南地區各自的儲層結構特點用不同的方法取得了當地的m值，現對其進行比較（表1）。由表1可以看出，這些地區的儲層都是具有裂縫和孔洞的複雜孔隙儲層，孔隙類型、結構多樣化，儲集空間具有很強的非均質性。地區不同m值也不同，但變化不是很大，均為1.699~2.53，而且不同組段不同儲層類型的m值也不相同，三類儲層的m值小些，一類、二類儲層的m值較大。

表 1 不同地區求取的m 值對比表

（2）m值的影響因素及變化規律

以普光2井飛仙關組上段儲層岩心樣品51個，飛仙關組下段儲層岩心樣品82個，毛壩2井飛仙關組儲層岩心樣品11個，毛壩3井長興組儲層岩心樣品37個，普光6井和普光8井的8塊岩心總計189塊岩心樣品做岩電分析實驗。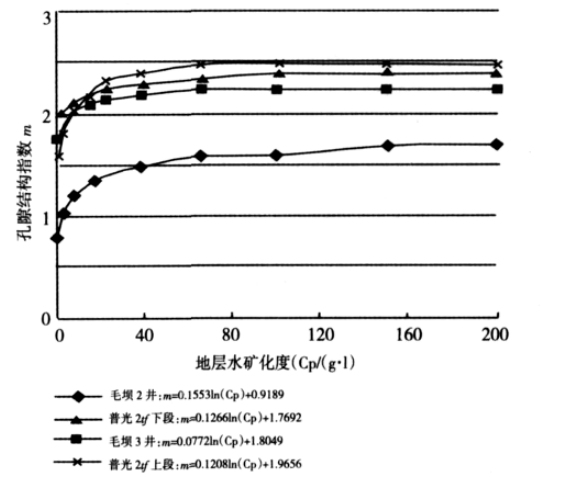

圖1 孔隙結構指數 m 與地層水礦化度 Cp 的關係圖

分析結果表明，孔隙結構指數m與孔、洞、縫的發育有直接關係。孔隙結構指數m的總體趨勢是隨孔隙度增大而增大；孔隙度與滲透率相關性好的儲層，孔隙結構指數隨孔隙度增大而增大幅度較小，孔隙度與滲透率相關性差的儲層，孔隙結構指數隨孔隙度增大而增大幅度要大一些，即均質性好的孔隙（洞）型儲層，孔隙結構指數受孔隙度大小影響較小，而非均質性較強的縫洞型儲層，孔隙結構指數受孔隙度大小影響較大；溶孔、溶洞越發育，孔隙結構指數越高，裂縫越發育，孔隙結構指數越低。

岩電實驗結果還表明，m值隨地層水礦化度的增大而呈增大趨勢，礦化度大於80g/L後，m值隨礦化度的增大而呈增大趨勢；地層水礦化度變化平緩時，m值變化不大；地層水礦化度相同時，泥質含量的多少對m值也有影響，泥質含量越高m值越小，這是通過對岩心補償陽離子濃度的測試得到的，其主要是由泥質的附加導電性造成的（圖1）。當地層水礦化度相同時，地面溫度下測得的m值高於地層溫度（123℃）下測得的m值；地層水礦化度越低，兩者的差異越大；隨地層水礦化度的增加，兩者的差異逐漸減小（表2）。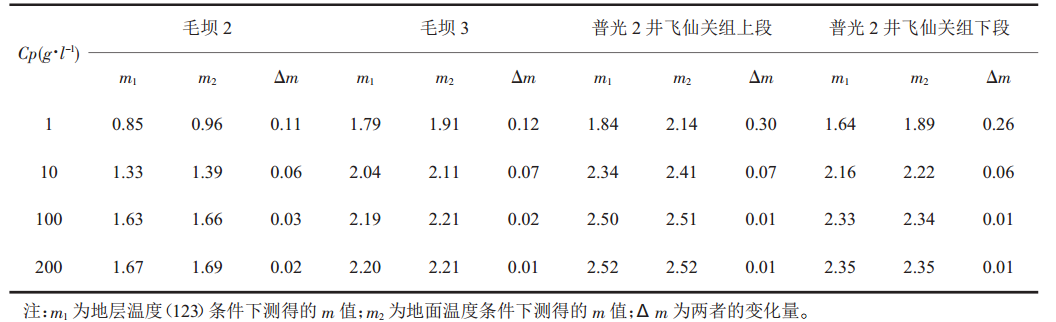

表 2 地層水礦化度、 溫度變化對岩心 m 的影響

基於孔隙模型的孔隙儲層膠結指數值

由於縫洞性儲層的複雜性，各地區針對各自的地質特點建立了各自物理解釋模型，比較典型的如雙孔隙模型和三孔隙模型，雙孔隙模型有分別針對非連通孔洞和裂縫/連通孔洞各自的模型。

（1）模型類型及套用研究

Aguilera發表了用於雙孔隙系統，即基質和不連通孔洞以及基質和裂縫/連通孔洞組合的精確公式，Aguilera提出了適用於基質、裂縫和不連通孔洞任意組合的三孔隙模型。潘保芝教授對孔隙模型Ⅰ、雙孔隙模型Ⅱ和三孔隙模型的不同孔隙組合進行了詳細的說明和推導，並介紹了孔隙模型的具體進展。

①雙孔隙模型Ⅰ。把岩石孔隙分為基質孔隙和非連通孔洞孔隙，各部分用串聯電阻網路來模擬，用於計算具有非連通孔洞儲層的孔隙指數m的值。

②雙孔隙模型Ⅱ。把岩石孔隙分為基質孔隙和裂縫/連通孔洞，兩部分孔隙之間用並聯電阻網路來模擬，用於計算裂縫儲層m的值，或者具有連通孔洞儲層m的值。

圖2 孔隙模型電阻網路關係圖

③三孔隙模型。岩石孔隙由非連通孔洞、裂縫和基質孔隙組成，可以用基質孔隙與裂縫的並聯，再與非連通孔洞串聯的電阻網路來模擬（圖2）。

研究結果表明，三孔隙模型適合於單孔隙、雙孔隙和三孔隙系統的所有組合，如果改變岩石骨架，還可獲得火山岩、碳酸鹽岩和砂岩等各種岩性三重孔隙結構解釋模型。王青也對孔隙模型做過研究，他的三孔隙模型和Aguilera建立的三孔隙模型有所不同，他認為，在無裂縫溝通時，孔洞的存在只是增大了孔隙度，對岩石電導率影響不大，在建立模型時，把孔洞孔隙和基質孔隙視為一體，稱為基質孔洞孔隙，岩石的導電性可以由裂縫導電網路與基質孔洞孔隙導電網路並聯來模擬，圖3為該模型的導電示意圖。該模型同樣適用於各種岩性剖面和各種儲層的測井解釋模型。

（2）孔隙模型推導m值的影響因素

孔隙模型推導m值雖然在一些地區取得了很好的套用效果，但是也存在一定的局限性，這些模型都是基於巨觀岩石等價模型建立的，因此，把儲集層岩石導電這一複雜問題過於理想化了，從而不足以揭示地層電阻率的物理本質。模型的實際套用依賴於現代能夠對複雜儲層合理表征的測量儀器，因為在理論公式推導過程中，未考慮電流的傳導方式，而其傳導方式依賴於很多因素，例如，電阻率儀器的測量方式等。因此，對於模型的套用需做進一步研究。

圖3 三重孔隙度測井解釋模型

用測井資料推導膠結指數值

利用測井資料求取m值，主要是交會裂縫孔隙、總孔隙和電阻率資料對複雜孔隙儲層m的求取，關鍵在於如何獲得較準確的裂縫孔隙和總孔隙數值。對裂縫孔隙度的計算還沒有特別成熟的方法，傳統的有根據雙孔介質模型，用中子孔隙度與聲波孔隙度之差來計算裂縫孔隙度，但需要一定的條件，只有當地層孔隙度較高並且不含氣時才較為合適，因此，該方法在很多地區都不合適。雙側向電阻率不論是油層還是氣層都正好突出了裂縫的作用。基於此，國內外趨同於用深、淺側向電阻率計算裂縫孔隙度，並建立了各自的計算解釋模型。

在生產測井中，該方法是一種確定m值的間接方法，它不像岩電實驗方法那樣直接，會受到許多因素的制約，如受到已有測井曲線的限制，而且還要進行多條曲線的遞歸分析，計算量較大。利用測井資料確定複雜孔隙儲層m值往往還會受到泥質含量的影響，只有泥質校正後的資料才具有較好的套用價值，泥質含量的校正也直接關係到m值的精確度。

研究結論

基於岩電實驗求取m值相對來說實現起來比較容易，但受地區影響很大，而且可變膠結指數不僅受孔隙結構的影響，還受地層水礦化度的影響，這樣當區塊地層礦化度變化比較大時，難以進行套用。而通過建立孔隙模型求取m值實現難度比較大，但是具有一定的通用性，能夠更全面地反映地層複雜的導電機理。根據各自模型考慮的導電因素以及各導電因素的導電關係不同又可以分為不同的模型，只有全面考慮各種導電因素並在模型中正確的反映各個導電因素之間的關係的導電模型，才具有很強的通用性。當然，作為套用型的解釋方法，不可能考慮所有的因素，參數太多就沒法套用，考慮太少又反映不了實際情況，套用效果會變差。因此，應找到一個能較全面反映各個因素又不引入過多參數的方法是準確確定複雜空隙儲層膠結指數m值的關鍵。

膠結指數的控制因素及評價方法

利用Archie公式計算儲層含水飽和度時，膠結指數通常是某一層位取某一固定值。岩電實驗結果表明，不同地層的膠結指數並不相同，其大小隨孔隙結構和泥質含量的變化而變化。由於膠結指數受孔隙結構和泥質含量等多種因素的控制，因此，必須首先利用岩電實驗數據和泥質指示測井結果，採用多元回歸分析法建立膠結指數的計算模型；然後利用測井數據，根據建立的計算模型確定各目的層的膠結指數。力求使計算的膠結指數儘可能逼近實際值，以保證利用Archie公式計算的儲層含水飽和度具有較高的準確性。

膠結指數的控制因素

（1）岩石的電阻

在地層中，天然氣、石油和岩石骨架幾乎是不導電的，某些金屬礦物雖可導電，但由於其含量非常小，以至於對整個岩石的導電性幾乎不產生影響，而實際上真正起導電作用的是泥質和孔隙流體。所以，岩石的電阻可以看作是泥質和孔隙流體2個電阻並聯的結果。

（2）完全含水純砂岩的電阻率

根據毛管理論：完全含水純砂岩的電阻可以看成是許多長度相同而半徑不同含水毛管電阻的並聯；含水毛管中流體的電阻率是自由水與束縛水的綜合回響，它與地層水電阻率、地層水粘度、地層水中鹽類離子的遷移率及毛管粗細等因素有關

（3）膠結指數的控制因素

對於不含泥質的砂岩，其膠結指數與岩石孔隙度、地層水電阻率、地層水水性係數、岩石孔隙彎曲度、毛管視平均截面積及毛管半徑等因素有關。泥質砂岩中，分散於岩石孔隙中的泥質會影響岩石的孔隙彎曲度、毛管視平均截面積及毛管半徑。連續分布的泥質由於具有一定的導電性，從而影響完全含水岩石的電阻率（相當於並聯了一個電阻）。所以，泥質地層的膠結指數除與上述因素有關外，還與泥質數量、泥質的分布形式等有關。對於某一地區的某一層位而言，地層水電阻率和地層水水性係數都可以認為是不變的，所以，在某一特定的層位可以不考慮地層水電阻率和地層水水性係數引起膠結指數的變化。孔隙彎曲度、毛管視平均截面積及毛管半徑控制著岩石的滲透率，它們可以用滲透率來描述。所以，岩石膠結指數的主要控制因素為孔隙度、滲透率和泥質含量。孔隙度和滲透率又是岩石孔隙結構的一種表象。因此，簡單地說就是孔隙結構和泥質含量控制著岩石膠結指數的大小。

控制因素對膠結指數的影響

（1）孔隙結構對膠結指數的影響

實驗證明：具有相同孔隙結構的純砂岩，其地層因素的對數與孔隙度的對數之間具有近似的直線關係（直線的截距為a值的對數，斜率為m值），而不同孔隙結構的岩石，其直線的斜率及截距不同，即a值、m值不同。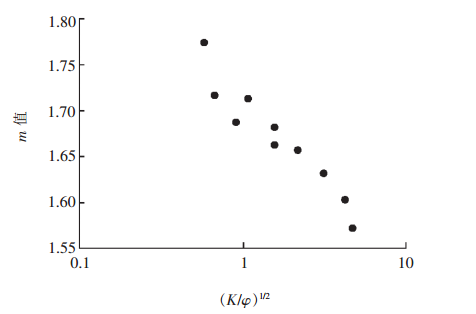

圖4 膠結指數與孔隙結構指數的關係

岩石的孔隙結構用孔隙結構指數來描述。孔隙結構對膠結指數的影響一般在純砂岩或泥質含量較低的砂岩儲層中進行考察。圖4是塔里木某油田A3井部分泥質含量較低的地層中m值（a取常數1時）與孔隙結構指數的關係。可以看出：孔隙結構指數越小（岩石的孔隙結構越複雜），對應的m值則越大。

（2）泥質含量對膠結指數的影響

泥質對岩石導電性的影響取決於泥質含量及分布形式。當泥質含量較低時，泥質主要以分散形式存在於孔隙及喉道之中，使岩石的孔隙空間減小（孔隙度變小），孔隙喉道變得迂迴曲折甚至堵塞（使孔隙彎曲度變大、毛管半徑變小），從而使岩石的導電性變差；當泥質含量較高時，一部分泥質分散於孔隙及喉道之中，使岩石儲集性能變差（孔隙度變小、孔隙結構變複雜），岩石的導電性變差，而另一部分泥質形成連續分布，構成導電通路，使岩石的導電性變好（相當於並聯了一個電阻）。泥質對膠結指數的影響相對較為複雜。大量的岩電實驗結果表明，泥質含量與膠結指數的關係整體呈如圖2的三段式變化，但不同地區的不同層位，3條線段彼此交叉的位置存在差異。其總體規律是：①泥質含量較低時，連續分布的泥質很少（甚至沒有），它們主要使孔隙度變小、孔隙結構變複雜、岩石的導電性變差，m值（a取常數1時）隨泥質含量增大而增大；②隨著泥質含量的增加，連續分布的泥質增多，它將逐漸抵消部分泥質使孔隙度變小、孔隙結構變複雜而導致岩石導電性變差，在某一範圍內兩者基本處於平衡，m值（a取常數1時）隨泥質含量的變化較小（或基本不變）；③當泥質含量增加到一定程度之後，連續分布的泥質對岩石導電性的影響起主導作用，從而使m值（a取常數1時）隨泥質含量增大而減小。

膠結指數的確定方法

由於膠結指數受孔隙度、滲透率和泥質含量等多種因素的控制，所以，膠結指數與任一單因素的相關性都不是特別好（用單因素確定膠結指數必定引起較大誤差）。因此，必須採用多因素回歸分析的方法進行擬合，力求使計算的膠結指數儘可能逼近岩石的實際值。膠結指數的確定方法為：首先利用岩電實驗數據和泥質指示測井，採用多因素回歸分析法建立其計算模型；然後利用測井數據，根據建立的計算模型確定目的層的膠結指數。

研究結論

（1）利用Archie公式計算儲層的含水飽和度時，係數a和膠結指數的大小隨孔隙結構和泥質含量的變化而變化（不同地層的a值、m值不同）。

（2）在a取常數1時，岩石的孔隙結構越複雜（孔隙結構指數越小），對應的m值越大。

（3）泥質對膠結指數的影響相對較為複雜。泥質含量與膠結指數的關係整體呈三段式變化。

（4）在確定膠結指數時，應首先利用岩電實驗數據和泥質指示測井，採用多元回歸分析法建立其計算模型，然後利用測井數據，根據建立的計算模型進而確定出目的層的膠結指數。