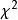耶茨連續性修正

耶茨連續性修正是在皮爾遜χ²統計量K_n，r的計算公式中，若ν_i<E_i，則用ν_i+0.5代替μ_i;若ν_i>E_i，則將ν_i換成ν_i-0.5。當觀測次數n充分大時，修正與不修正差別微小。連續性修正是耶茨(F.Yates)1934年針對如下事實提出的： 皮爾遜χ²統計量K_n，r的分布是離散型的，而χ²分布是連續型的，故稱做 “連續性”修正。

基本介紹

• 中文名：耶茨連續性修正
• 外文名：Yates Continuity Correction 
• 所屬學科：數學（統計學）
• 提出者：耶茨(F.Yates)
• 相關概念：皮爾遜χ2統計量Kn，r

基本介紹

檢驗的基礎是泊松分布和二項機率分布的正態近似。因為前二個分布是離散的，後一個分布是連續的，會有輕微的偏斜。這種情況可使用所謂“耶茨連續性修正”。使用這個修正規則，值應按下列公式來計算{讀作“O與E之差的絕對值”。只是指兩值之差，不管符號。)

一般不值得使用耶茨連續性修正，除非在2×2表中期望的元素頻數對任一元素都少於5.0。

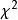
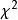
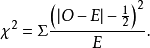
相關分析

2×2表的卡方檢驗

一般的2×2表可以寫成表1中所示的型式。計算統計量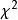的常用表達式為：

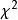
對於2×2表，簡化成如下形式：

表1 一般的2×2列聯表

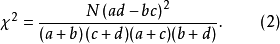
		變 量 A
		類 1	類 2
變數B	類 1	a	b	a+b
	類 2	c	d	c+d
		a+c	b+d	N=a+b+c+d

上面的統計量的顯著性是通過比較它與自由度為1的表查卡方值而得以判斷。

Yates連續性修正

推導統計量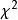的分布時是用一連續機率分布(即卡方分布)作為對觀測頻數之分立機率分布(即多項分布)的近似，為改善此近似，Yates(1934)提出了一個修正，它包括取平方之前將正偏差(觀測-期望)減0.5，負偏差時加0.5。這個修正可直接併入公式(2)，變為：

稱為修正連續性後的卡方值。公式(3)中，項表示的絕對值，即此表達式的數值，而不管它的符號。

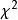
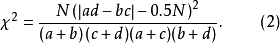
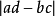
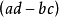
近來對Yates修正的優點已有一些討論。Conover(1968，1974)對它在所有情況下的常規使用提出了異議，但Mantel和Greenhouse(1968)，Fleiss(1973)及Mantel(1974)不同意他的意見。總的來說，贊成套用此修正的證據似乎是有力的，因此它的使用。當然，如果樣本足夠大，這個修正對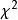值將不產生什麼影響。