群論在化學中的套用

美國著名無機化學家科頓（ F. A. Cotton ）教授在多年教學基礎上為初學群論的化學工作者撰寫的入門書——《群論在化學中的套用》（“ Chemical Applications of Group Theory ”）。

該書簡明扼要、通俗易懂，避免了繁瑣的數學推理，結合實例進行了詳細的討論，闡述了群論的基本原理和方法，並詳細介紹了群論在化學領域的各方面的套用。

基本介紹

• 書名：群論在化學中的套用
• 作者：F.A.Cotton
• 原版名稱：Chemical Applications of Group Theory
• 譯者：劉萬春 游效曾 賴伍江
• ISBN：7-5335-1553-6
• 定價：35.00元
• 出版社：福建科學技術出版社
• 出版時間：1999年10月
• 開本：787×1029 mm 1/16

主要內容

原理

化學研究的對象是分子。分子的幾何構型和對稱性，是分子的重要性質。套用群論知識，就能得到某些確定的結果。

群的性質　水分子的兩個O—H鍵成某一確定的角，設σ為HO所在的平面,σ尙為通過的平分線並垂直於σ的平面,c為σ尙與σ的交線（圖1）。
通過σ、σ尙的鏡面反映或繞c軸轉動180°,水分子的幾何構型不變。用代表“不動”,叫做單位元素,於是、c、σ、σ尙這四個元素就構成了一個集合,記作c。
對水分子先施加σ,再施加σ,兩次作用的結果與一次施加c的結果一樣,則說明c為σ尙與σ之積,記作c=σ尙σ。集合c有以下性質：
① c中任何兩個元素之積皆在c中。
② 對於c中的任意三個元素A、B、C，記作A、B、C∈c，下式就成立：(AB)C=A(BC)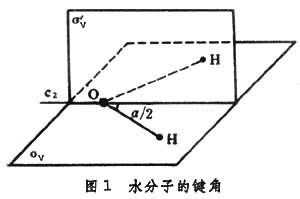

群論在化學中的套用

③ 有單位元素,使得。
④ c中的任何一個元素,都有逆元素,也在c中，使得。
有上述四條性質的集合c,就叫做一個群，稱之為c群。在c下水分子的幾何構型不變，就說水分子具有c對稱性。一般情況下,群元素的乘法是不可交換的，雖然對c來說是可交換的。
群的表示方法　設氧的p軌道沿著c方向，p、p分別位於σ、σ尙平面上(圖2)，則在c的元素的作用下，這些軌道按下列規則變化：
　　式中D(A)為與A相應的三階方陣。把群元素A與對應的矩陣D(A)列成表1。這一組矩陣叫做c的一個表示，記作。矩陣的階數（這裡是3）叫做表示的維數，(p，p，p)為表示的基底。由這些矩陣對角元之和組成的一組數稱為表示的特徵標，記作。
可以看到，這組矩陣已經約化成由對角線上的小矩陣組成的矩陣，則說是可約的表示。這些相同位置上的小矩陣，又構成c的幾個表示,於是得到表2（省略表示矩陣的圓括弧）。
由於B、B、A皆為一維表示,它們的特徵標與表示是一樣的，因此也把表示的特徵標列在同一表中。
顯然，B、B、A不能進一步約化，即它們是不可約的表示，其中A表示嶕(A)皆為1，稱為全對稱表示。從表2可驗證：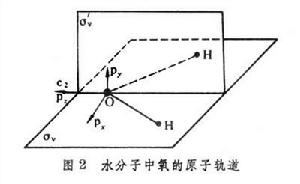

群論在化學中的套用

群論在化學中的套用

群論在化學中的套用

群論在化學中的套用

(1)

式中α、β為群c的不可約表示,為群的階,對c,=4。
由式(1)可得一個表示向不可約表示分解的規則：

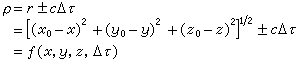群論在化學中的套用

(2)

式中，則，例如：=B+B+A表示的直接和。已經得到在基底p、p下c的兩個不可約表示B、B,則在pp、pp下，容易得到、的新的表示,如表3所示,則說明、分別是B與B和B與B的直接乘積,記作：

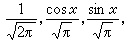群論在化學中的套用

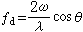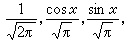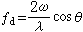群論在化學中的套用

群論在化學中的套用

群論在化學中的套用

Γ1=B1×B1

一般情況下,或是可約的，在本例中,=A,=A是不約的,是B和B均為一維表示的緣故。顯然,=，，一般有：
也可證明，兩個相同的不可約表示的直接乘積包含一個而且只含一個全對稱表示，而兩個不同的不可約表示的直接乘積不包含全對稱表示。

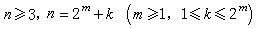群論在化學中的套用

群論在化學中的套用

群論在化學中的套用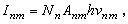

群論在化學中的套用

套用

群論在化學中的套用舉例　在雜化軌道理論中，要討論可能有哪些雜化以使中央原子與配位體形成具有某種對稱性的分子，例如構想要構造一個有O對稱性的分子,設6個配位體的18個p軌道中的6個p軌道指向中央原子，其餘的p軌道垂直於中心方向，於是這18個p軌道被分成兩組，以期與中央原子分別形成σ鍵和π鍵。以這兩組矢量為基底得到了O的兩個表示和π，如表4。
由O的特徵標表和(2)式得到：

群論在化學中的套用

σ=A1g+Eg+T1u

π=T1g+T1u+T2g+T2u

式中A、E、T、T、T、T
為電子組態(見配位場理論)。在中央原子只能提供s、p、d軌道的情況下，s、、(p，p，p)分別屬於A、E、T，因而可以形成spd雜化(且說明是哪兩上d軌道參與雜化)，與周圍配體的p軌道相匹配形成σ鍵；而(p，p，p)、(d，d，d)分別屬於T和T，還有T和T沒有相應的軌道提供，則不可能發生形成π鍵的雜化。

群論在化學中的套用

出版背景

自1832 年伽羅華（ E. Galois ）初步描述了群的數學概念後，經過很多數學家的補充、完善，至今群論已發展成為數學的一個分支。儘管群論是一門抽象的數學，但其基本理論與物質結構的具體對稱性結合之後就成為研究和認識物質微觀運動規律的一種有力工具。在有關基本粒子、核結構、原子結構、分子結構以及晶體結構等問題的理論研究和計算中經常用到群論方法，同時也促進了群論的發展。由於自然科學各學科間的交叉、滲透，在近代化學領域內研究化學鍵理論、晶體學、分子動力學以及各種波譜學等都離不開群論知識。

美國著名無機化學家科頓（ F. A. Cotton ）教授在多年教學基礎上為初學群論的化學工作者撰寫的入門書——《群論在化學中的套用》（“ Chemical Applicationsof Group Theory”） 被譯成多國文字。其第二版(1991, John Wiley ）已在20 多年前由我們譯成中文。其特點是通俗易懂，避免了不必要的繁瑣的數學推導，並結合實例進行討論，對問題的敘述比較具體。該中譯本於1975 年出版後立即被大學化學系和有關科研院所列為大學生和研究生學習群論的基本參考書或教材。

1990 年該書第三版問世，在內容上較第二版有重要修改和補充。此後不久，科頓教授訪華，譯者有幸與他會晤，獲允翻譯其第三版。隨後，科頓教授寄來習題解答和他應邀為第三版中譯本撰寫的序言。多年來科頓教授為中國培養了不少高級科研人材，此次放棄版稅無疑是對中國科教事業的又一貢獻。