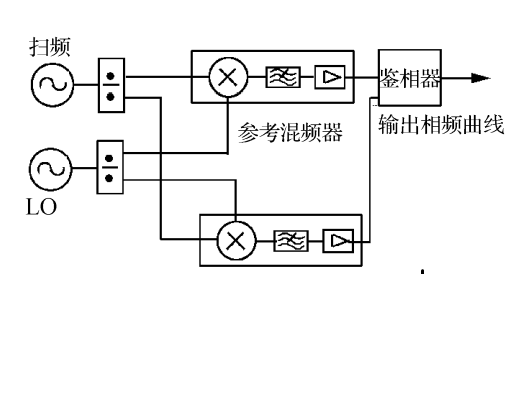
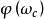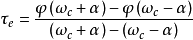介紹
群時延是通信系統和網路中一項重要傳輸特性,它表征系統和網路的線性失真。群時延是指群信號通過線性系統或線性網路時,信號整體產生的時延,它是合成波包絡的傳播時間,所以也稱包絡時延。群時延一方面指傳輸信號必須是群信號,如AM、FM、PM信號以及電視信號或數字調製信號,單色波傳輸無群時延可言。另一方面,群時延是波群整體的時延,而不是某個頻率分量的相時延,也不是各分量的相時延的平均值。從物理意義上說,某一頻率的群時延表示以該頻率為中心的一個很窄頻帶內的信號通過系統和網路的傳輸時間,在數值上等於相位特性的一階微分。
單一的正弦信號是無法攜帶信息的,實際有用信號如:音頻、視頻或數據不是單一的正弦信號,而是由一指定頻率範圍內的頻率群所組成。這一群複雜波通過網路後在其輸出端所產生的相位時延是各不相同的,這些形狀基本相同且頻率亦在同一指定波段內的正弦信號重疊所形成的各信號在網路兩點間傳播的時間就是群時延。群時延在網路相頻特性曲線上的幾何意義如右圖 所示。
 相頻特性曲線測試示意圖
相頻特性曲線測試示意圖推導
下面是一個線性網路的群時延的數學表達式推導:
 系統時域頻域關係圖
系統時域頻域關係圖其中,f(t)為系統的輸入時間信號,h(t)為系統的脈衝回響,g(t)系統的輸出時間信號,F(jw)為f(t)的譜度數,H(jw)為系統的轉移函式,G(jw)為系統輸出信號的譜密度函式。
相關術語
相位延時
對於一個線性網路 (如信道 )的傳遞函式可以寫成
,式中。A(w)為線性網路的幅頻特性;
為線性網路的相頻特性;
為正弦信號的角頻率。單一正弦信號通過線性網 絡後總會產生相位滯後,對應於相位滯後的時間即是相位時延,表示為波的相移對角頻率之比.
由於相位測量具有 2
模糊性, 所以相位時延並不是正弦波在網路中傳播時間。相位時延在網路相頻特性曲線上的幾何意義如右圖 a所示。
 相位時延
相位時延包絡時延
如果通過網路的信號不是簡單的正弦波,而是經過一群頻率(例如聲波或視頻)調製後的已調波,那么包絡產生的失真稱為包絡失真,所產生的時延稱為包絡時延。如果調製頻率為
載波頻率為
調製後在載頻左右形成上邊頻
和下邊頻
 包絡時延
包絡時延Ω這三個頻率成分通過網路產生的相移分別為
、
和
則根據相移與角頻率之比的關係,得到包絡時延的公式
包絡時延在網路相頻特性曲線上的幾何意義如右圖c所示。當已調波占用頻帶內的相移 特性是線性關係, 此時的包絡時延在數值上就是等於群時延。
主要缺點
難以避免矛盾
測量準確度和測試精度是傳統群時延測試方法本身固有的矛盾, 這是實際工程套用中對群時延測試最難以把握的地方.一般而言,都是對準確度和精度折衷考慮,以犧牲一定精度為代價換取相對準確可信的測試結果.傳統的群時延定義和測量方法得到的是各個頻點的群時延, 反映的是一個局部概念, 難以與一定頻寬內的信號時延建立關係.因而傳統方法定義和測量的群時延難以與信號時延建立對應關係 沒有清晰的物理概念, 不便於在工程實踐中套用.
難以反映特性
群時延是描述系統相位線性度的整體概念, 傳統群時延基於微分( 差分) 的定義抹煞了這一點. 當群時延為線性時, 各頻點的群時延一樣; 但是當系統呈非線性相位特性時, 各頻點傳統定義的群時延不同, 難以得到信號頻寬內的整體群時延, 難以與擴頻信號傳輸時延建立對應關係.實際傳輸網路都不同程度的存在色散, 也就是時延隨信號頻率發生變化, 反映在相位特性上即是非線性相位系統. 混頻器、功放、低噪放等設備都是非線性相位系統, 擴頻信號經過這些系統時會產生相位畸變.
 相頻特性曲線測試示意圖
相頻特性曲線測試示意圖 系統時域頻域關係圖
系統時域頻域關係圖




 相位時延
相位時延
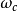



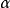
 包絡時延
包絡時延