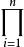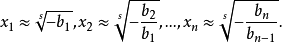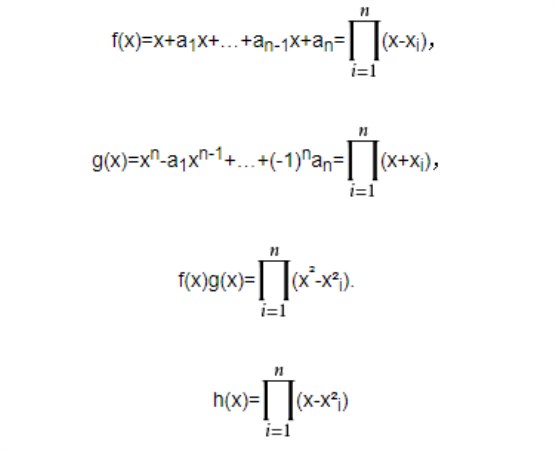羅巴切夫斯基方法

羅巴切夫斯基方法(Lobachevski method)是求多項式復根近似值的一種方法。設方程為f(x)≡a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n=0，而其首項係數a₀=1。這個方法就是作出一系列的新方程，使每一方程的根恰是前一方程各根的平方。最後得到一個方程，它的各根的絕對值彼此相差甚大，以致從這方程的係數就很容易看出它的根。這方法的一個優點是能一次把所有的根都求出來。可利用羅巴切夫斯基方法求方程複數根的近似值，只是計算更加複雜，而求實根的近似值按近似公式即可。羅巴切夫斯基方法是羅巴切夫斯基在其著作《代數，有限計算》 (1834)中提出的。羅巴切夫斯基方法在有的書刊文獻中又稱作丹德林方法——以比利時數學家丹德林(G.Dandelin，1794-1847)命名，丹德林與羅巴切夫斷基是彼此獨立發現此法的。

基本介紹

• 中文名：羅巴切夫斯基方法
• 外文名：Lobachevski method
• 別稱：羅巴切夫斯基-格雷費方法
• 所屬學科：數學
• 所屬問題：高等代數(多項式)

基本介紹

羅巴切夫斯基方法是求多項式復根近似值的一種方法，設

f(x)=x+a₁x+…+a_n-1x+a_n=(x-x_i)，

則

g(x)=xⁿ-a₁x^n-1+…+(-1)ⁿa_n=(x+x_i)，

且

f(x)g(x)=(x²-x²_i).

於是

h(x)=(x-x²_i)

是以f(x)的根的平方x²₁，x²₂，…，x²_n為根的n次多項式，同樣可求出以x⁴₁，x⁴₂，…，x⁴_n為根的n次多項式等。

羅巴切夫斯基方法的基本思想

可用以下特殊情況來說明羅巴切夫斯基方法的基本思想，設x₁，x₂，…，x_n都是實數，且|x₁|>|x₂|>…>|x_n|，又s是一個充分大的正整數，而

K(x)=xⁿ+b₁x^n-1+…+b_n-1x+b_n=(x-x^s_i)，

從而-b₁=x^s₁+x^s₂+…+x^s_n，b₂=x^s₁x^s₂+x^s₂x^s₃+…+x^s_n-1x^s_n，…，(-1)ⁿb_n=x^s₁x^s₂…x^s_n，於是當s充分大時，x^s₁≈-b₁，x^s₁x^s₂≈b₂，…，x^s₁x^s₂…x^s_n=(-1)ⁿb_n，因此，

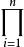
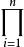
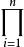
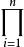
羅巴切夫斯基(Н.И.Лобачевский)在1834年所著《代數》一書中提出這一方法，此法也被格雷費(K.H.Gräffe)在1837年獨立提出，因此，這種方法也稱為羅巴切夫斯基-格雷費方法。