按照宇宙學原理在宇宙學尺度上天體系統最重要的特徵之一是均勻性和各向同性。H.P.羅伯遜和沃爾克分別於1935年和1936年證明,適應於上述均勻性和各向同性要求的四維時空只有三種,它們的時空度規具有右圖形式。
基本介紹
- 中文名:羅伯遜-沃爾克度規
- 外文名:Robertson-Walker metric
- 提出者:H.P.羅伯遜和沃爾克
- 提出時間:1935和1936年
- 套用學科:宇宙學
- 適用領域範圍:描述天體系統的特徵
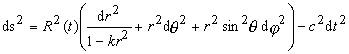
按照宇宙學原理在宇宙學尺度上天體系統最重要的特徵之一是均勻性和各向同性。H.P.羅伯遜和沃爾克分別於1935年和1936年證明,適應於上述均勻性和各向同性要求的四維時空只有三種,它們的時空度規具有右圖形式。
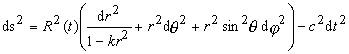
H.P.羅伯遜和沃爾克分別於1935年和1936年證明,適應於上述均勻性和各向同性要求的四維時空只有三種,它們的時空度規具有右圖形式。中文名 羅伯遜-沃爾克度規 外文名...
羅伯遜-沃克度規(英語:Robertson-Walker metric)是H.P.羅伯遜和沃爾克分別於1935年和1936年證明的。由於俄國數學家弗里德曼和比利時物理學家勒梅特也作出了重要的...
羅伯遜-沃克度規是H.P.羅伯遜和沃爾克分別於1935年和1936年證明的。由於俄國數學家弗里德曼和比利時物理學家勒梅特也作出了重要的貢獻,因此也稱作弗里德曼-羅伯遜-...
這個經修改的愛因斯坦場方程具有一個各向同性並均勻的解:弗里德曼-勒梅特-羅伯遜-沃爾克度規,在這個解的基礎上物理學家建立了從一百四十億年前熾熱的大爆炸中演化...
參見:弗里德曼-勒梅特-羅伯遜-沃爾克度規弗里德曼方程所基於的假設是宇宙在空間上是均一且各向同性的;從今天的經驗來看,這個假設在大於一億秒差距的尺度上是合理的...
同年,勒梅特發表了愛因斯坦場方程的一個嚴格解,這個解後來被稱為弗里德曼-勒梅特-羅伯遜-沃爾克度規,並由此指出宇宙是膨脹的,最初起源於一個“原始原子”的爆炸...
平坦性問題是一個與弗里德曼-勒梅特-羅伯遜-沃爾克度規相關的觀測問題。...... 平坦性問題是一個與弗里德曼-勒梅特-羅伯遜-沃爾克度規相關的觀測問題。...
R(t)稱為宇宙距離標度因子。當k=+1時,R(t)稱為宇宙半徑;因為這時我們可以把羅伯遜-沃爾克度規的空間部分當作四維歐氏空間中半徑為R(t)的超球面。而當k=0...
它們最早由亞歷山大·弗里德曼在1922年得出,他通過在弗里德曼-勒梅特-羅伯遜-沃爾克度規下對具有給定質量密度和壓力的流體的能量-動量張量套用愛因斯坦引力場方程而得到...
從羅伯遜-沃爾克度規,作為一級近似,可以得到速度-距離間的線性關係。霍金斯、斯特芬森、維爾茨和陸啟鏗等許多學者,分別根據不同的宇宙模型得出紅移與距離的平方成正比...
模型採用了弗里德曼-勒梅特-羅伯遜-沃爾克度規、弗里德曼方程和宇宙的狀態方程來描述從暴脹時期之後至今以及未來的宇宙。 [1] 重子聲學振盪暗能量 編輯 在...
根據宇宙學原理可以推導出演化態宇宙的羅伯遜-沃爾克度規。運用完全宇宙學原理則能得到穩恆態宇宙度規,利用不同的度規可建立各種宇宙模型。...
加入宇宙學常數後,宇宙學標準羅伯遜-沃爾克度規可以導出Λ-冷暗物質模型,後者因與觀測結果的精確吻合而被稱為宇宙“標準模型”。暗物質被認為是當今形式化宇宙循環...
根據宇宙學原理,在大尺度上度規應當是均勻且各向同性的,唯一符合這一要求的度規叫做弗里德曼-勒梅特-羅伯遜-沃爾克度規(FLRW度規)。這一度規包含一個含時的尺度...
根據宇宙可以推導出演化態宇宙學的羅伯遜-沃爾克度規。運用完全宇宙學原理則能得到穩恆態宇宙學度規,利用不同的度規可建立各種宇宙模型。V百科往期回顧 詞條統計 ...
與物理學中,特別是在微分幾何與廣義相對論中,扭曲幾何(warped geometry)是度規...許多愛因斯坦場方程的基本解是為扭曲幾何,比如史瓦西解以及羅伯遜-沃爾克模型。...
以紅移z(或lgz,或lgcz)為縱坐標,視星等m為橫坐標,可以繪製紅移-視星等圖,通常稱為哈勃圖。根據羅伯遜-沃爾克度規,可以算出紅移z和視星等m之間的近似關係:...
特別是的孤立子(soliton)解可被展示:其包含了輻射主導形式(早期宇宙)與物質主導形式(晚期宇宙)中的羅伯遜-沃爾克度規(Robertson-Walker metric)。一般方程式則可被...
以宇宙學原理為前提,採用共動坐標系,把空-時的描述分解為空間的描述和時間的描述而得到羅伯遜-沃爾克度規:式中r,θ,嗞為球面坐標,R(t)為宇宙標度因子,k為...
正比於這些星系的紅移(redshift),這一膨脹宇宙的觀點也在1927年被勒梅特在理論上通過求解弗里德曼方程而提出,這個解後來被稱作弗里德曼-勒梅特-羅伯遜-沃爾克度規。...
同年,勒梅特發表了愛因斯坦場方程的一個嚴格解,這個解後來被稱為弗里德曼-勒梅特-羅伯遜-沃爾克度規,並由此指出宇宙是膨脹的,最初起源於一個“原始原子”的爆炸...
星系的距離正比於這些星系的紅移,這一膨脹宇宙的觀點也在1927年被勒梅特在理論上通過求解弗里德曼方程而提出,這個解後來被稱作弗里德曼-勒梅特-羅伯遜-沃爾克度規。...
1922年發現了廣義相對論引力場方程的一個重要的解,即弗里德曼-勒梅特-羅伯遜-沃爾克度規。1924年他在發表的論文闡述了膨脹宇宙的思想,即曲率分別為正、負、零時...
