置換多面體

置換多面體(permutation polytope)是一個與置換有關的多面體。作一個圖，它的頂點是X={1，2，…，n}上的n!個置換，它的兩個頂點f與g有一條邊相連的充要條件是：存在一個對換t，使f=t·g，這種圖可以用凸多面體來表示，稱它為一個置換多面體。

基本介紹

• 中文名：置換多面體
• 外文名：permutation polytope
• 所屬學科：數學
• 所屬問題：組合學（組合多面形與最最佳化)
• 簡介：一個與置換有關的多面體

基本介紹

設是一個給定的向量，且規定，設S_n為上的所有置換的集合，對於每個置換，將它與點聯繫，點集

在n維歐氏空間E_n中的凸包稱為置換多面體，並記它為。例如，若兩個向量和滿足關係：

和存在兩個置換使得

對於，則稱x由y所管制，並記為。拉多定理指出：，若且唯若，由此，置換多面體由如下的方程和不等式組的解集所確定：對任何，

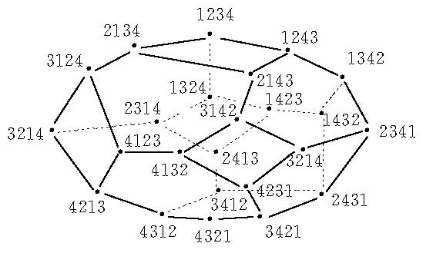
圖1 置換多面體

偶置換多面體

S_n可以劃分為奇置換的集合S與偶置換的集合S，即，集合的凸包稱為偶置換多面體，並用表示，若且唯若，而且對於任何滿足

其中

例如，圖2給出，這裡。

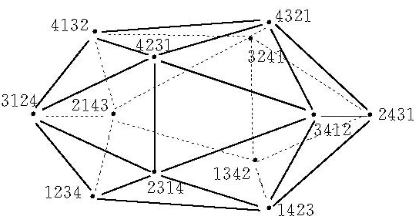
圖2 偶置換多面體