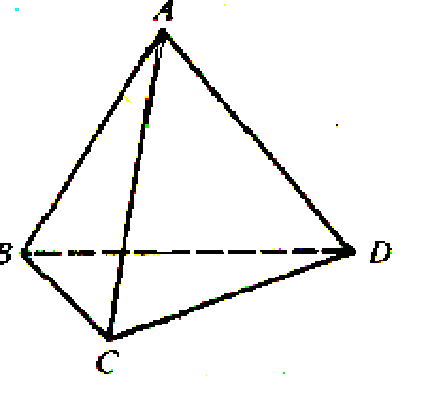
多面體染色是組合數學中一類常見問題。其大致題意為:對於一個正多面體,用一定種類的顏色對其表面、頂點或(和)邊進行染色。若兩種染色方案可以通過旋轉對應,則視其為同一染色方案。題目希望求得對於給定條件下,不同染色可能的方案數目。注意,本文所指多面體染色和圖著色問題為兩類完全不同的問題。
多面體染色問題一般可通過波利亞定理與burnside引理求解。
基本介紹
- 中文名:多面體染色
- 外文名:Polyhedron Coloring
問題定義
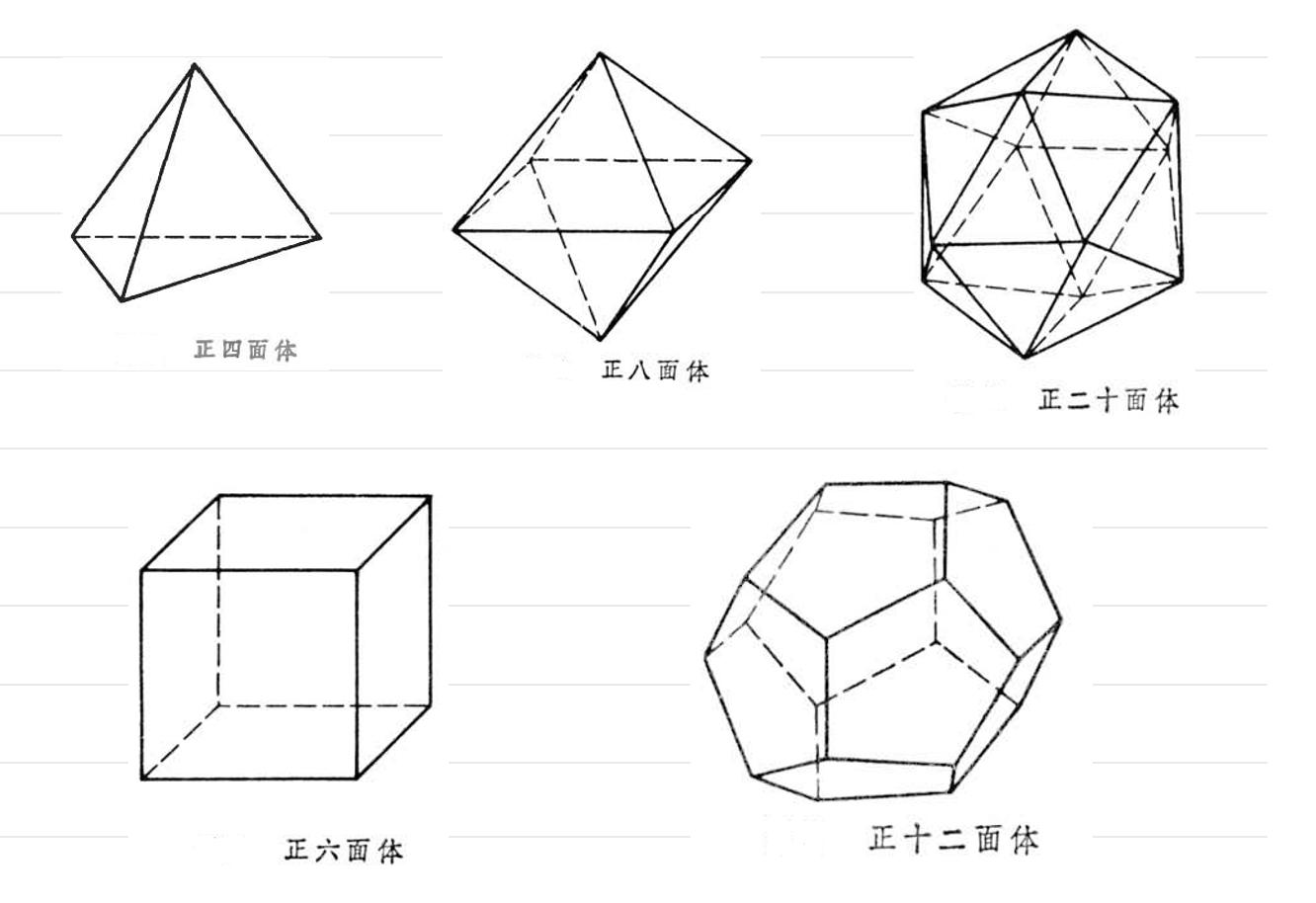
問題解法


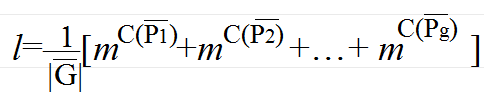
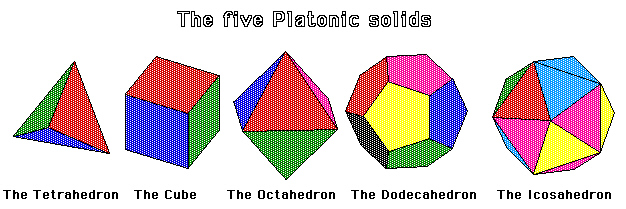
例題
置換類型 | 置換數量 | 循環表示 |
不動置換 | 1個置換 |  |
面面中心轉±90度 | 2*3個置換 |  |
面面中心轉180度 | 3個置換 |  |
棱中對棱中轉180度 | 6個置換 |  |
對角線為軸轉±120度 | 2*4個置換 |  |

置換類型 | 置換數量 | 不動點個數 |
不動置換 | 1個置換 | 6!個不動點 |
面面中心轉±90度 | 2*3個置換 | 無不動點 |
面面中心轉180度 | 3個置換 | 無不動點 |
棱中對棱中轉180度 | 6個置換 | 無不動點 |
對角線為軸轉±120度 | 2*4個置換 | 無不動點 |

置換類型 | 置換解釋 | 置換數量 | 循環表示 |
不動旋轉 | - | 1個置換 |  |
以頂點與對面的中心連線為軸按反時針方向旋轉±120度 | 置換(BCD)與(BDC)。置換(ACD)與(ADC),置換(ABD)及(ADB),(ABC)及(ACB )所對應的旋轉。 | 8個置換 |  |
以正四面體的3對對邊之中點聯線為旋轉軸旋轉180度 | (AB)(CD),(AC)(BD),(AD)(BC) | 3個置換 |  |