緯圓

緯圓(latitudinal circle)是迴轉面上的一種圓，迴轉面上任一點的軌跡是圓，這些圓通常稱為緯圓，也稱為緯線。

基本介紹

• 中文名：緯圓
• 外文名：latitudinal circle
• 所屬學科：數學
• 所屬問題：立體幾何
• 簡介：迴轉面上的一種圓
• 別稱：緯線

基本介紹

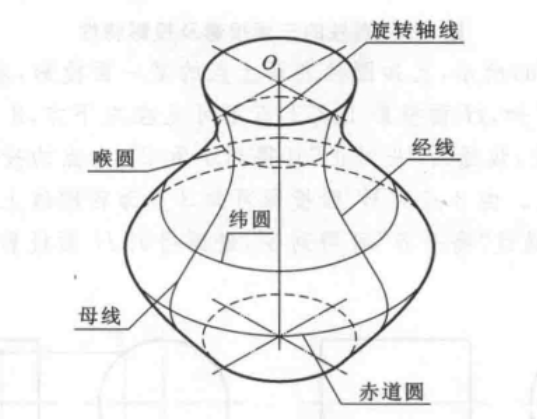
曲面是由直線或曲線按照一定規律運動形成的軌跡；迴轉曲面是由一條母線，這條母線可以是直線，也可以是曲線，繞一固定軸線即直線旋轉一周所形成的曲面。由曲面或主要由曲面圍成的立體稱為曲面立體，由平面圖形繞與其共面的軸線迴轉形成的立體稱為迴轉體，其表面為迴轉曲面或迴轉曲面和平面，如圖1所示。

從迴轉體的形成可知，母線上任意一點的運動軌跡都是圓，這個圓稱為緯圓，最大半徑的緯圓稱為赤道圓，最小半徑的緯圓稱為喉圓。緯圓所在的平面必與旋轉軸線垂直。

圖1 迴轉體的形成

圖2

緯圓法求定點問題

圖2為正圓錐的三面投影圖，所謂正圓錐是指圓錐的底面與迴轉軸垂直。

圖2（a）

分析圖2所示圓錐體可以看出，圓錐體底面在正面投影和側面投影中積聚，如果點在底面上，點的投影容易確定。但是如果點在圓錐的側面上，由於側面在三個投影中均沒有積聚性，與平面上定點一樣，需要在面內通過作輔助線確定點的投影。理論上可以在曲面上作任意輔助線確定點的投影，但是為了保證求解的準確性，只有直線和圓周可以利用。利用曲面上的直素線求解體上定點問題的方法稱為素線法。利用曲面上的緯圓求解體上定點問題的方法稱為緯圓法。下面通過例題介紹求解過程。

【例1】已知A點在圓錐體上，如圖3所示，試補全A點的三面投影。

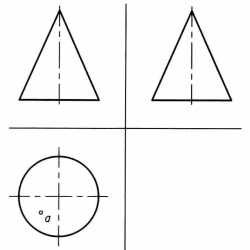圖 3

解： 下面用緯圓法求解A點的正面投影和側面投影：

在水平投影中以s為圓心，過a點作圓，該圓為圓錐的緯圓，如圖4(a)所示。 由緯圓的水平投影作正面投影，如圖4(b)所示。A點在緯圓上，因此A點的正面投影a'在緯圓的正面投影上，由此得到A點的正面投影a'，如圖4(c)所示。再依據A點的水平投影a和正面投影a'求出側面投影a''，如圖4(d)所示。