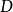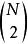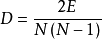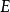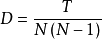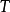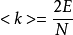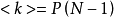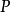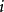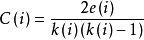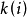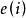簡單的說,網路科學（Network Science）應該是專門研究複雜網路系統的定性和定量規律的一門嶄新的交叉科學,研究涉及到複雜網路的各種拓撲結構及其性質,與動力學特性(或功能)之間相互關係,包括時空斑圖的湧現、動力學同步及其產生機制,網路上各種動力學行為和信息的傳播、預測(搜尋)與控制,以及工程實際所需的網路設計原理及其套用研究,其交叉研究內容十分廣泛而豐富。
基本介紹
- 中文名：網路科學
- 外文名：Network Science
- 專門研究：複雜網路系統的定性和定量規律
- 相關：與動力學特性(或功能)間相互關係
發展簡史,網路屬性,套用範圍,
發展簡史
圖論和拓撲學
網路科學首先得益於圖論和拓撲學等套用數學的發展。關於圖論的文字記載最早出現在歐拉1736年的論著中,他所考慮的原始問題具有很強的實際背景。在數學上,關於哥尼斯堡七橋問題、多面體的歐拉定理、四色問題等都是拓撲學發展史的重要問題。而在歐拉身後，一些數學大師如柯西、漢密爾頓、凱利、基爾霍夫、波利亞等都對圖論作出了貢獻，使這門科學得到了快速的發展。
1、哥尼斯堡七橋問題
哥尼斯堡是東普魯士的首都,今俄羅斯加里寧格勒市,普萊格爾河橫貫其中。18世紀在這條河上建有七座橋,將河中間的兩個島和河岸連結起來。人們閒暇時經常在這上邊散步,有人提出:能不能每座橋都只走一遍,最後又回到原來的位置。這個看起來很簡單卻很有趣的問題吸引了大家,很多人在嘗試各種各樣的走法,然而無數次的嘗試都沒有成功。誰也沒有做到,看來要得到一個明確、理想的答案決非那么容易。
1736年,有人帶著這個問題找到了當時的大數學家歐拉,歐拉經過一番思考,很快就用一種獨特的方法給出了解答。歐拉首先把這個問題簡化,他把兩座小島和河的兩岸分別看作四個點,而把七座橋看作這四個點之間的連線.歐拉圖的研究開創了“圖論”這門新的數學分支[7],因此,這是第一代科學家對網路的開創性貢獻,於是歐拉被譽為圖論之父。問題是要從這四塊陸地中任何一塊開始,通過每一座橋正好一次,再回到起點。即這個問題就簡化成,能不能用一筆就把這個圖形畫出來。經過進一步的分析,歐拉得出結論———不可能每座橋都走一遍,最後回到原來的位置。並且給出了所有能夠一筆畫出來的圖形所應具有的條件。這是拓撲學的“先聲”。歐拉在1736年解決了這個問題,他用抽象分析法將這個問題化為第一個圖論問題:即把每一塊陸地用一個點來代替,將每一座橋用聯接相應的兩個點的一條線來代替,從而相當於得到一個圖。歐拉證明了這個問題沒有解,並且推廣了這個問題,給出了對於一個給定的圖可以某種方式走遍的判定法則。這項工作使歐拉成為圖論〔及拓撲學〕的創始人。因此,關於哥尼斯堡七橋問題、多面體的歐拉定理、四色問題等成為拓撲學發展史上的著名問題。
2、四色問題（四色定理）
在圖論的歷史中,還有一個最著名的問題———四色猜想（四色定理）。提出四色猜想的人來自英國,有一段有趣的歷史。1852年,畢業於倫敦大學的弗南西斯.格思里來到一家科研單位搞地圖著色工作時,發現了一種有趣的現象:“看來,每幅地圖都可以用四種顏色著色,使得有共同邊界的國家都被著上不同的顏色。”每個國家必須由一個單連通域構成,而兩個國家相鄰是指它們有一段公共的邊界,而不僅僅只有一個公共點。1872年,英國當時最著名的數學家凱利正式向倫敦數學學會提出了這個問題,於是四色猜想成了世界數學界關注的問題,它是圖論中的一個著名的問題,並且是世界近代三大數學難題之一。世界上許多一流的數學家都紛紛參加了四色猜想的大會戰。1878~1880年兩年間,著名律師兼數學家肯普和泰勒兩人分別提交了證明四色猜想的論文,宣布證明了四色定理。但後來數學家赫伍德以自己的精確計算指出肯普的證明是錯誤的。不久,泰勒的證明也被人們否定了。於是,人們開始認識到,這個貌似容易的題目,其實是一個可與費馬猜想相媲美的難題。所以它對圖的著色理論、平面圖理論、代數拓撲圖論等分支的發展起到推動作用。進入20世紀以來,科學家們對四色猜想的證明基本上是按照肯普的想法在進行。電子計算機問世以後,由於演算速度迅速提高,加之人機對話的出現,大大加快了對四色猜想證明的進程。1976年,美國數學家阿佩爾與哈肯在美國伊利諾斯大學的兩台不同的電子計算機上,用了1200個小時,作了100億判斷,終於完成了四色定理的證明。當然,不少數學家還在探索一種更簡捷明快的書面證明方法。
隨機圖理論
兩個匈牙利著名的數學家Paul Edo''s(保羅·愛爾德)和Alfred Renyi（阿爾弗雷德·萊利）,他們在20世紀50年代末和60年代合作發表了8篇論文，這8篇論文在歷史上首次探討了我們所處的相互關聯的宇宙的基本問題：網路是如何形成的？建立了著名的隨機圖理論,奠定了隨機網路理論的基礎。這一理論最重要的假設為：網路節點之間的連結是隨機選擇建立連線的。他們認為網路圖和它所代表的世界從根本上說是隨機的。隨機網路模型的前提是深刻的平等主義：我們完全隨機的安排連結，因此所有的節點都有等同的機會獲得連結。
他們用相對簡單的隨機圖來描述網路,簡稱ER隨機圖理論,他們的最重要發現是ER隨機圖中許多重要性質都是隨著網路規模的增大突然湧現的。他們創立的ER隨機圖理論為圖類的閾函式和巨大分支湧現的相變等提供了研究網路,的一種重要的數學理論。
確實,用圖論的語言和符號可以精確簡潔地加以描述各種網路,圖論不僅為數學家和物理學家提供了描述網路的共同語言和研究平台,而且至今圖論的許多研究成果、結論和方法技巧仍然能夠自然地套用到現在複雜網路的研究中去,成為網路科學研究的有力方法和工具之一。在長達40年的ER隨機圖對於圖論理論的影響大而廣泛。
小世界理論和六度分離
1998年,科學家迎來了複雜網路的又一次突破性進展,首先衝破了ER理論的框框的人是,美國康奈爾(Cornell )大學理論和套用力學系的博士生Watts及其導師Strogatz在《Nature》雜誌上發表了題為《“小世界”網路的群體動力行為》的論文,提出了小世界網路模型。這實際上是20世紀60年代美國哈佛大學的心理學家Milgram曾經作過的著名的小世界實驗的一種拓廣,Milgram提出的“六度分離”(six degrees of separation )社會調查後的推斷,它原意是指在美國大多數人中,任意兩個人平均最多通過6個人就能夠彼此認識。不管是誰如果想認識一個素不相識的人,只要通過六個他的朋友的朋友轉達之後,一般就能夠聯繫得上。人們常有這么體驗,當參加國內外會議或訪問或旅遊時,經常與遇到一些新朋友交談時,你很快就發現:他認識你的朋友,你認識他的朋友的朋友,於是大家不約而同地脫口而出:這個世界真小啊!這就是“小世界效應(現象)”,這裡包含了“六度分離概念”的基本思想,那么你現在想與世界上任何一個人(例如史蒂芬·霍金等)聯繫交朋友嗎?咋看似乎不太可能。如果你真想聯絡到他,應該怎么辦?你可這樣做:找一個最有可能和他有聯繫的親友,把問候轉達給他,然後他也照樣去找下一位親友。這樣你一共需要多少個親友作為“中轉站”就能找到對方呢?這個問題的答案或許有點讓人吃驚:不論你想找地球上哪人(壯漢或名人),大約只需要6步,最後一步就是“中轉”的最終目標。2003年哥倫比亞大學社會學系的的瓦茨(DuncanWatts)領導的研究小組在《科學》雜誌上,發表實驗報告,他們利用網際網路在全世界範圍內初步檢驗了上述驚人的假說,有六萬多志願者參與利用電子郵件通信試驗,例如從分布世界各地某同學的同學進行通信試驗表明,確實不到6步就實現了,這是利用網際網路初步驗證了小世界現象。但是這個試驗還不夠多,他們準備做上億的網際網路進一步試驗。可見,Watts和Strogatz的研究結果進一步揭示了複雜網路的小世界效應。
無標度網路模型（Scale-free Network）
1999年美國聖母(Notre Dame )大學物理系的Barabási教授(見圖1.3)及其博士生Albert在《Science》雜誌上發表了題為《隨機網路中標度的湧現》一文[3],提出了一個無標度網路模型,發現了複雜網路的無標度性質,並和M. Newmann,D. J. Watts共同編輯了“網路的結構與動力學”(The Structure and Dynamics,普林斯頓大學出版社,普林斯頓, 2003年)專著,該書在國際上產生了廣泛的影響,引起了全世界的高度重視。正是他在網路科學方面的傑出貢獻,因此於2006年獲得了美國von Neumann (馮紐曼)計算金獎。
標誌著複雜網路研究進入了網路科學的新時代,由此誕生了一門嶄新的科學:網路科學。網路科學的二大發現,以及隨後許多真實網路的實證研究表明,真實世界網路既不是規則網路,也不是隨機網路,而是兼具小世界和無標度特性,具有與規則網路和隨機圖完全不同的統計特性。這在全世界學術界激起了千重浪,複雜網路文章鋪天蓋地,網路科學的綜述和專著不斷湧現[11~22],從物理學到生物學,從社會科學到技術網路,從工程技術到經濟管理等眾多領域,受到了人們的空前的廣泛關注和重視,正在突飛猛進。
網路屬性
度
對於一個節點，若看作源節點，
出度：由源節點指向其他節點的邊數；
入度：其他節點指向源節點的邊數；
度：出度與入度的和。
密度：
網路密度
是網路中已有的邊數與總的可能存在的邊數的比率，（通俗說就是現有的邊數與所有的點都連線的邊數的比值）。對於一個有N個節點的無向圖網路，理論上邊數最大為
，則密度
，其中
是圖中存在的邊，對於一個有向圖網路，密度
，其中
是單向的邊。
平均度：
網路圖的平均度和密度有著密切的關係，其平均度
，在ER隨機圖模型中,我們可以計算
其中
是連線兩個節點的機率。
平均路徑長度(Average path length)
平均路徑長度：首先計算通過尋找所有成對的節點之間的最短路徑長度，然後把它們的長度求和，然後除以總對數，就是平均路徑長度。這告訴我們平均路徑長度是一個節點到網路中的另一個節點所要走的平均長度。
網路直徑(Diameter of a network)
作為測量網路圖的另一個度量標準，我們可以定義網路直徑為網路中最短路徑的最大值，換句話說，首先計算每個節點到其他節點的最短路徑，則網路直徑就是最短路徑的最大值。直徑代表著線性網路的大小。
聚集係數(Clustering coefficient)
聚類係數是測量“all-my-friends-know-each-other”。通常被描述為我的朋友的朋友還是我的朋友。更準確的是，一個節點的聚類係數是這個節點存在的連線點數與最大可能的連線點數的比值，一個網路整體的聚類係數是各個節點聚類係數的取平均值，同時具有小的平均路徑和高的群聚係數，就形成了小世界效應。
則
節點的聚類是
，其中
是鄰居節點的數量，
是鄰居節點的鄰居的連線數，則鄰居節點的最大連線數為
。
連通性
連通性扮演者重要的作用在分析和解釋網路的連通性時，圖根據連通性被歸類在四個不同的類別:
- 派系/完全圖：所有節點都能連線到其他所有節點的圖是一個完全連通圖。如果所有節點都有其他全部節點的內部連結和外部連結，則這個網路都是對稱的。
- 最大連通子圖：最大的連通分支。
- 弱連通圖：一個節點集合中存在任何其他節點都能相互到達的路徑，忽略邊的方向性。
- 強連通圖：一個節點集合中存在任何節點都能相互到達路徑，需要考慮邊的方向性。
套用範圍
安全和軍事套用
網路拓撲結構的穩健性與脆弱性問題。例如建立能夠應對核打擊的軍事指揮網路。網路結構對軍事網路的容錯性影響，軍事網路的抗干擾、多環境、多任務、異構性、保密性研究均涉及網路科學。如怎么確保複雜網路可靠運轉以有效應對網路災變?如何應對未來虛擬攻擊帶來的嚴重後果？我們參考。2009年Stuxnet病毒攻擊伊朗核設施的事件、2011年“CSDN泄密門”事件就會看到這類研究的重要性。
生物和疾病控制
如何控制計算機病毒和各種傳染病傳播(包括:愛滋病、非典和禽流感等)以應對給人類造成巨大的威脅?網路科學對於研究傳染病的傳播方式有著重要的作用。不同的網路模型對於我們的應對方式有著不同的指導原則。例如在隨機網路中，傳統的疾病傳播理論認為，每種病毒都有一個傳播閾值，超過這個閾值，疾病會傳播。而在無標度模型中，則這一閾值消逝，疾病的傳播與中心節點的攜帶病毒的概論有關。
物聯網研究等其它
物聯網在未來將會成為一個全球性的動態網路。其覆蓋面將無限大，功能繁多，網路異構性強、覆蓋面廣、信息處理能力強，跨越虛擬和現實空間，因為會成為一個複雜網路的研究樣本。對於其發展，一方面需要藉助網路科學的研究成果加以引導和控制，另一方面又可以作為網路科學的研究樣本促進這一學科的發展。
