維納一霍普夫方程(Wiener-Hopf equation)是一種帶差核的奇異積分方程。
古典的維納一霍普夫方程是指下述的帶差核的奇異積分方程
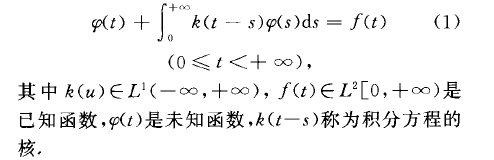
方程(1)的研究開始於20世紀20年代初,早期著名例子是輻射傳輸理論中的米爾恩方程,後因1931年由維納(Wiener,N.)和霍普夫(Hopf , E.)給出求解方法而得名.20世紀40年代以後,這種方程的理論在解析函式邊值問題、調和分析和運算元理論的基礎上得到了系統的發展,20世紀60年代以後,抽象化為奇異積分方程的一種統一形式,即一般的維納一霍普夫方程的理論.它的套用也擴展到許多其他領域,如中子遷移、電磁波衍射、控制論、多體問題以及人口理論等.維納和霍普夫為解方程(1)提出的方法後來被稱為維納一霍普夫技巧,又稱為因子分解法.其基本思想是通過積分變換將原方程化為黎曼邊值問題.技巧的核心是用函式因子分解的方法求得方程的解.下面以方程(1)求解為例加以說明.在xG0處令抓x) =.f (x)=0,將方程(1)延拓到整個實軸,得到


