維納-霍普夫積分方程是由於研究輻射遷移理論的需要而提出的一類積分方程,是實際套用中經常遇到的,但不完全滿足古典的弗雷德霍姆理論的方程。
基本介紹
- 中文名:維納-霍普夫積分方程
- 外文名:Wiener- Hopf integralequations
- 適用範圍:數理科學
簡介,發展,理論基礎,發現聯繫,完整化,
簡介
維納-霍普夫積分方程是由於研究輻射遷移理論的需要而提出的一類積分方程。
下面的線性積分方程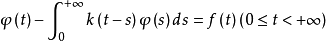 稱為維納-霍普夫積分方程。
稱為維納-霍普夫積分方程。
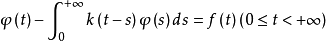
發展
理論基礎
維納-霍普夫積分方程是實際套用中經常遇到的,但不完全滿足古典的弗雷德霍姆理論的方程。由於研究輻射遷移理論的需要,從20世紀20年代起就開始了對這一類型方程的研究。
關於方程
在維納與霍普夫的上述工作中,第一次利用了因子分解的思想來處理方程。
由研究維納-霍普夫方程而逐漸發展起來的維納-霍普夫技巧(即因子分解的技巧),現在已經成為研究維納-霍普夫方程的重要的理論基礎,而且也是研究許多數學物理問題的強有力的工具。
發現聯繫
關於方程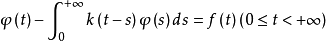 的第二個重要結果是由拉普潑特於1948年得出的。他在假定核k(t)滿足適當的條件,把方程化成一個黎曼邊值問題,從而藉助黎曼邊值問題的一些熟知結果對方程進行研究。在上述工作中,拉普潑特建立了方程在函式類L2(0,+∞)中的正則可解性定理,並且第一次指出了指數
的第二個重要結果是由拉普潑特於1948年得出的。他在假定核k(t)滿足適當的條件,把方程化成一個黎曼邊值問題,從而藉助黎曼邊值問題的一些熟知結果對方程進行研究。在上述工作中,拉普潑特建立了方程在函式類L2(0,+∞)中的正則可解性定理,並且第一次指出了指數
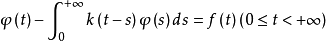


完整化
1958年,克列因和哥赫別格等人進一步發展了維納-霍普夫的因子分解的思想,對方程建立了更為一般和更加完整的理論。
