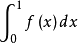維塔利-哈恩-薩克斯定理

簡介

維塔利-哈恩-薩克斯定理是測度論的重要定理。

設(Ω,𝓕,μ)是測度空間，{μ_n}是定義在𝓕上的具有有限全變差（即|μ_n|(Ω)<+∞,n=1,2,...）的複測度列，v是𝓕上的測度。如果每個μ_n關於v絕對連續，且對任何A∈𝓕，v(A)<δ時，有|μ_n|(A)<ε(n=1,2,...)。

維塔利-哈恩-薩克斯定理有著悠久的歷史。

1907年，維塔利證明了若{f_n}是[0,1]上的(L)可積函式列，幾乎處處收斂於函式f，則

和

存在且相等的充分必要條件是{f_n}中的積分一致絕對連續。

1922年，哈恩證明了若{f_n}是[0,1]上的(L)可積函式列，且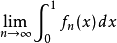

對每個(L)可測集A⊂[0,1]都存在，則{f_n}的積分一致絕對連續，且

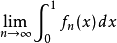收斂於一個集函式。

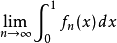
1933年，薩克斯把它推廣到一般的測度空間。

測度論是研究一般集合上的測度和積分的理論。它是勒貝格測度和勒貝格積分理論的進一步抽象和發展，又稱為抽象測度論或抽象積分論，是現代分析數學中重要工具之一。測度理論是實變函式論的基礎。

測度理論是實變函式論的基礎。所謂測度，通俗的講就是測量幾何區域的尺度。我們知道直線上的閉區間的測度就是通常的線段長度；平面上一個閉圓盤的測度就是它的面積。