維克定理

維克定理由吉安·卡羅·威克提出，在量子場論中廣泛用於將創生及湮滅算符的連乘積轉化為該連乘積的正規序與相應的收縮之和，在格林函式方法和費曼圖的相關問題中有重要套用。

基本介紹

• 中文名：維克定理
• 外文名：Wick's theorem
• 提出者：吉安·卡羅·威克
• 套用學科：量子力學術語
• 範疇：數理科學
• 涉及：真空態期望值

概念

維克定理由吉安·卡羅·威克提出，在量子場論中廣泛用於將創生及湮滅算符的連乘積轉化為該連乘積的正規序與相應的收縮之和，在格林函式方法和費曼圖的相關問題中有重要套用。

維克定理在計算場算符的真空態期望值的時候很有用。因為所有正規乘積的真空態期望值為零，而任意兩個算符的收縮根據上面的定義是一個很容易計算的數值，故任意產生算符與湮滅算符的連乘積的真空態期望值可以很容易計算出來。

基本原理

我們考慮玻色算符的維克定理。兩個自由場算符之間的收縮定義為

將場算符拆成正頻和負頻兩部分之和。

首先考慮 的情形，此時

正規乘積展開後為

將上兩式相減可得到一個對易式，是 數，於是式子可化成

對於的情形，上式右邊中的和交換位置，合併以上結果便有

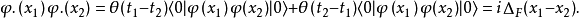
對於三個算符的情形，我們同樣先考慮的情形，得到

對於的情形，上式右邊後三項中的和交換位置，其他的時序關係可依次類推。把各種時序關係的貢獻加起來就得到

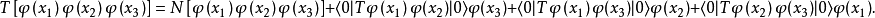
可利用歸納法不難得到玻色場的維克定理。