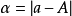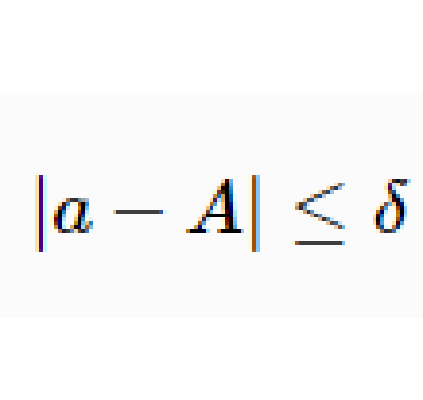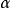絕對誤差界

絕對誤差界又稱為最大絕對誤差，是指絕對誤差的範圍。例如，用最小刻度是毫米的鋼尺來度量一個工件的長度，我們無法量得這個工件的準確數，因而也就無法求出這個近似數的絕對誤差，但是。這時我們可以確定測量結果的絕對誤差不超過1毫米。又如，若近似數8.27是由四捨五入法得到的，由於捨去或增加的不會超過0.005，因此，可以說8.27的絕對誤差界是0.005。再如，在生產中見到圖紙尺寸標準80^±0.5，在生活中見到火柴盒上寫有100^±2。±0.5，±2就是絕對誤差界。

基本介紹

• 中文名：絕對誤差界
• 外文名：bounds of absolute error  
• 別名：最大絕對誤差
• 相關概念：絕對誤差、相對誤差等

定理介紹

由於量值的準確數往往難以知道，因而絕對誤差也無法求得。但是，一般可根據具體問題估計出近似數與準確數最大可能相差多少，即可以定出絕對誤差的界限。

如圖1所示，用電壓表測量電源電壓(最小刻度單位為伏)，電源電壓的準確數A無法確定。但是，根據指針在7～8伏之間這一事實，當取a=8(伏)作為近似數時，可以斷定，近似數a與準確數A的絕對誤差不超過1伏，即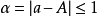 (伏)。進一步目測會發現，取近似數a=7(伏)，更為接近於準確數A；·並可知它和準確數A的絕對誤差不會超過刻度的半個單位，即a=7(伏)時。 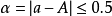(伏)。

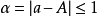
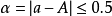
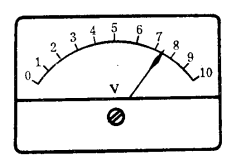圖1

因此，在度量一個量值時，雖然得不到準確數，但可以儘量使所取的近似數接近準確數，即使近似數的絕對誤差不超過所用量具上最小刻度的半個單位，這半個單位就可作為近似數的絕對誤差界限。

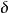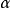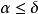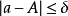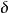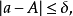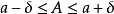定義 當準確數A無法知道時，如果找出一個儘量小的正數 ，使近似數 的絕對誤差 不超過它，即 或 ，則這個正數 稱為近似數a的絕對誤差界。由不等式 可得 ，其中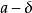 稱為準確數A的下界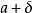， 稱為準確數A的上界。

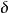
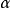
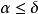
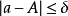
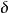
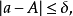
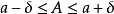
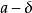
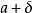
例題分析

測得某儀表指針長度的近似數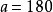 毫米，絕對誤差界 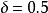毫米，求指針真實長度A的上界與下界。

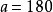
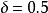
解：由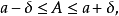 得：179.5毫米≤A≤180.5毫米。

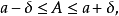
儀表指針的真實長度A的下界是179.5毫米，上界是180.5毫米，指針的真實長度介於179.5毫米與180.5毫米之間。

在生產實踐中，如製作一個線繞電阻的阻值要求是20歐姆，它的絕對誤差界為0.05歐姆，這表明要求所繞制的電阻阻值應在19.95歐姆與20.05歐姆之間，不在此範圍內的電阻就不合格。

習慣上，我們常把絕對誤差界附上正負號寫在近似數的後面，以表示近似數的精確度。例如測量某一零件尺寸為18.56(±0.005)毫米，表示該零件真實尺寸的近似值為18.56毫米，其精確度為±0.005毫米，零件的真實尺寸在18.555-18.565毫米之間。

絕對誤差

一個職工業餘學校共有學員1845名，如果把1800名作為學員人數的近似數，那么它比準確數少45名。

即 1800-1845=-45

如果用1900名作為學員人數的近似數，那么它比準確數多55名。

即 1900-1845=55

近似數與準確數的差值可能是正數，也可能是負數，但不論差值是正還是負，若它的絕對值越小，說明近似數與準確數越接近。上例中用近似數1800表示該校學員人數比用1900更接近實際情況，由此我們給出絕對誤差的定義。

定義 一個近似數 和它所代表的準確數A的差的絕對值，稱為這個近似數 的絕對誤差，用 表示，即 。

例1 用0.67作為 的近似值，它的絕對誤差是多少？

解：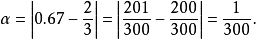

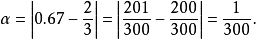
所以它的絕對誤差是。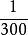

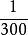
從等式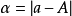中可以看到，絕對誤差是與近似數具有相同的單位。對於同一準確數A的不同近似數來說，絕對誤差越小的近似數，它的精確程度越好。