絕對穩定性研究在某種限制下的一類非線性系統為全局漸近穩定的條件,而通常意義下的穩定性則只局限於對具體的非線性系統個別進行分析。非線性特性可在一個限制類中任意選取時的非線性反饋系統的穩定性。研究控制系統的穩定性時提出的一種穩定性概念,具有非線性不確定性的控制系統的一種穩定性。
基本介紹
- 中文名:絕對穩定性
- 外文名:absolute stability
- 適用範圍:數理科學
簡介
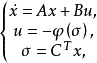
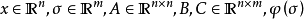
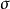

基本問題

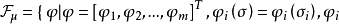
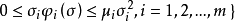
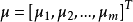
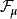
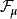

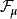

絕對穩定性研究在某種限制下的一類非線性系統為全局漸近穩定的條件,而通常意義下的穩定性則只局限於對具體的非線性系統個別進行分析。非線性特性可在一個限制類中任意選取時的非線性反饋系統的穩定性。研究控制系統的穩定性時提出的一種穩定性概念,具有非線性不確定性的控制系統的一種穩定性。
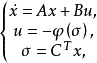
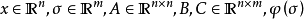
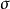


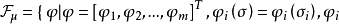
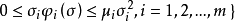
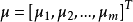
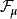
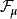

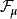
非線性特性可在一個限制類中任意選取時的非線性反饋系統的穩定性。研究控制系統的穩定性時提出的一種穩定性概念,具有非線性不確定性的控制系統的一種穩定性。...
絕對穩定,表示大氣的一種穩定狀態,是指在大氣層的溫度直減率γ小於氣塊的濕絕熱直減率γm的條件下,氣塊絕熱上升到某一高度,氣塊本身的溫度一定比四周空氣的溫度低...
穩定性是控制系統重要的性能指標之一,是系統正常工作的首要條件。穩定性包括絕對穩定性和相對穩定性,相對穩定性表征系統的穩定程度。對於線性定常系統而言,系統的相對...
對於非線性系統穩定性的判別,李雅普諾夫第二方法至今仍是主要的方法(見李雅普諾夫穩定性理論。李雅普諾夫方法還被套用於研究絕對穩定性和有限時間區間穩定性問題。...
定義:根據衡斂系統的狀態方程分析,系統(物質)的物理狀態變數為零時,系統(物質)具有穩定的物理狀態,這種表達系統(物質)物理狀態的穩定性是物理穩定性。...
剛性穩定性(stiff stability)一種考慮了方法精度的穩定性概念.以C記複數集合,對於正數D,a和B,定義集合如果數值方法是收斂的,且集合R,包含在該方法的絕對穩定區域...
數據穩定性(data stability)是衡量數據波動性與離散性的指標,數據波動越小,離散程度越小,則穩定性越高。通常以屬性評價值的熵作為數據穩定性的度量。...
穩定性係數在數學上稱為 “均方差變異係數”。其值是一個衡量相對離散程度的量。在保險學上,計算賠償基金均方差是用以表示實際支付的賠款較賠償基金可能多付或少...
不過,常見的穩定態,可認為適用多種過程。(4)世上沒有絕對的穩定態,即不可能表征量的取值“永遠”不隨時間而改變,故只要在足夠長的時間範圍內,符合穩定條件,就...
法律穩定性,是指法律在一定時期內不變更的屬性。法律是社會關係的調整器,社會關係的內容和性質都具有相對的穩定性,在一定的社會關係內容和性質發生變化之前,不能對...
結構穩定性(structural stability)突變理論的基本概念與基本問題.反映在近似相同的條件下,所得結果也近似相同的特性...
定義處於平衡位置的某一力學系統,在受到外力系的微小擾動後,仍能繼續處於平衡位置的性質。基本原理平衡位置系統的穩定性 當一個力學系統(或機械系統)受外力系的作用...
核穩定性是指原子核具有的阻礙自發衰變及裂變的能力。在天然及人工合成的2000多種核素中,只有近300種是穩定的,大部分是不穩定的。原子核的穩定性與原子核內的...
1 定義 2 穩定性判定 3 總結 穩定系統定義 穩定系統是指輸入有界,輸出必有界的系統。對線性時不變系統,若且唯若系統的單位脈衝回響h(n)絕對可和(或稱絕...
《穩定性與魯棒性的理論基礎》是一本正文語種為簡體中文的書籍。...... 5.1 線性系統的頻域穩定性判據5.2 絕對穩定性5.3 S過程的數學理論Ⅰ——頻域不等式...
膠體穩定性:潤滑脂抵抗分油的能力。...... 絕對值增加,溶膠重又穩定;再加入電解質,由於反離子的作用...在疏液膠體中加入高分子,往往顯著提高膠體的穩定性,稱為高...
Muffins-Sekerka界面穩定性理論是指晶體生長過程固液界面穩定性的線性動力學分析理論。...
剛性穩定是以政治權力的排他性和封閉性為基礎的政治穩定。剛性穩定是中國社會科學院農村發展研究所研究員于建嶸教授針對當下中國社會形勢進行解釋和總體把握時提出的。...
結構穩定是工程力學的一個分支,主要研究各種結構的穩定性,是工程結構安全性的重要內容之一。關於結構穩定問題的最初研究可以追溯到18世紀。...
勞斯判據(勞茨判據),又稱為代數穩定判據。勞斯於1877年提出的穩定性判據能夠判定一個多項式方程中是否存在位於複平面右半部的正根,而不必求解方程。由此勞斯獲得了...
