基本介紹
- 中文名：結構方程式
- 外文名：structural equation
- 就是：假定一組潛在變數中存在因果關係
- 存在：線性組合
- 採用：路徑圖（pathdiagram）的形式
- 套用領域：統計學
介紹,基本概念,模型的評價,結構方程模型的優點,
介紹
這一組潛在變數分別是那些觀測變數中的某幾個的線性組合。在技術上，通過驗證觀測變數之間的協方差，可以估計出這個基本線性回歸模型的係數值，從而在統計上檢驗所假設的模型對所研究的過程是否合適，也就是檢驗觀測變數的方差協方差矩陣與模型擬合後的引申方差協方差矩陣的擬和程度，如果證實所假設的模型合適，就可以得出結論：我們所假設的潛在變數之間的關係是合理的。
基本概念
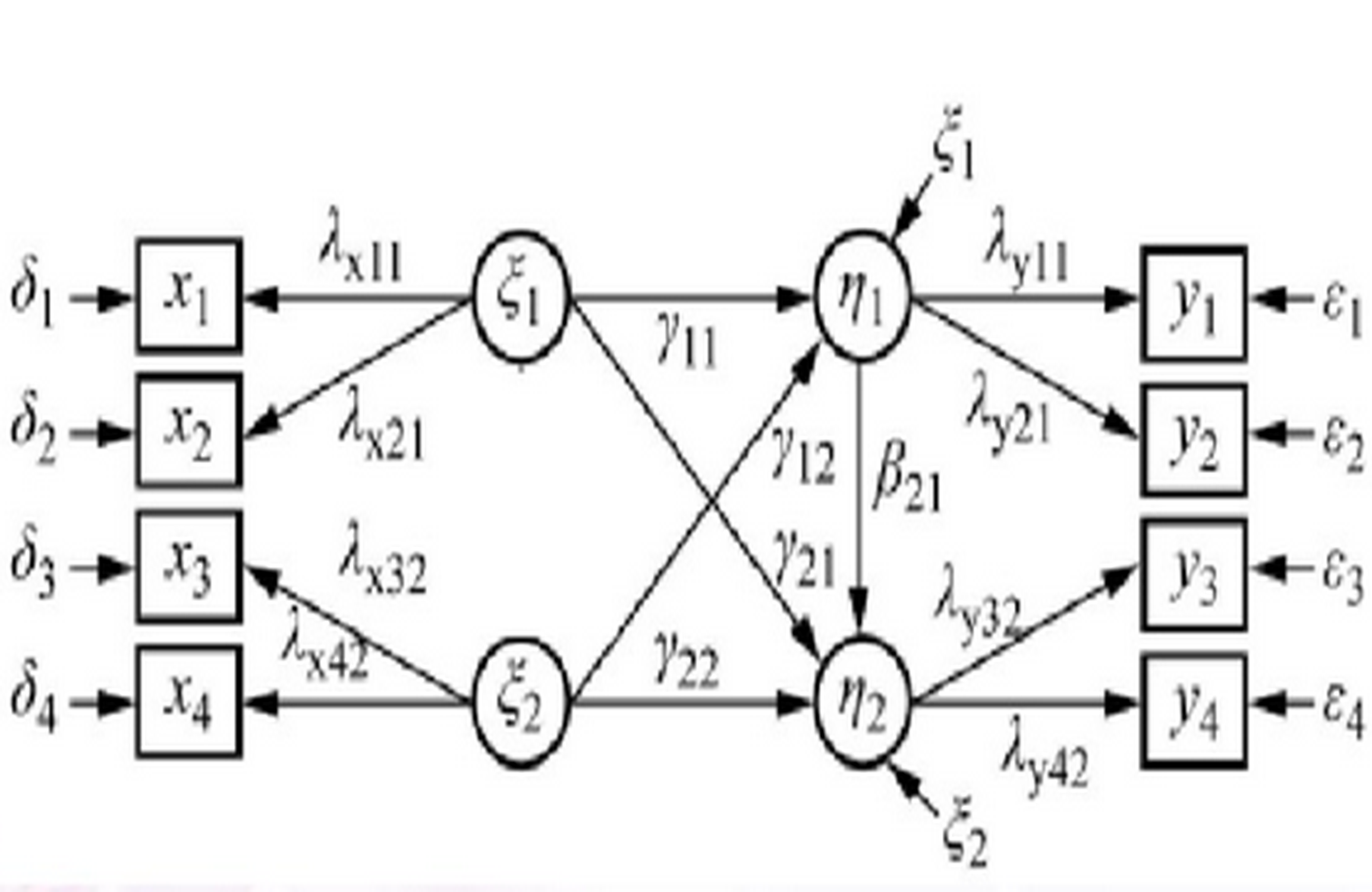
一般採用路徑圖（pathdiagram）的形式表示結構方程式模型，這是最簡單、最直觀的描述模型的方法，研究人員可以藉助路徑圖直接和明了地將變數之間的關係以圖形的方式表現出來。流行的AMOS軟體可以直接利用路徑圖的模型設定進行分析，並將分析結果直接標識在圖中。習慣上，在路徑圖中潛在變數用橢圓型表示，觀測變數用矩形表示；如果兩個潛在變數之間有相互關係，用雙箭頭聯結這兩個潛在變數；如果兩個潛在變數是因果關係，則用單箭頭聯結這兩個潛在變數，箭頭指向結果變數。如果一個潛在變數可由若干觀測變數表示，這個潛在變數被看作觀測變數的因子（factor），用單箭頭聯結這個潛在變數與觀測變數，箭頭指向觀測變數，表示潛在變數直接影響了觀測變數的值。在因果關係模型中，影響其它變數而其自身的變化又假定是由因果關係模型外部的其它因素所決定的變數稱之為外生變數（exogenousvariable），由外生變數和其它變數解釋的變數稱為內生變數（endogenousvariable）。
在SEM中，所假設的潛在變數之間的關係模型，是一種關於傳播理論的臨時的基本模型，我們稱之為結構模型（structuralmodel）；而那些在統計顯著的觀測變數與測量的潛在變數之間的線性關係模型，稱之為度量模型（measurementmodel）。結構模型實際上是某種意義上的回歸模型，要做的工作是驗證這個模型是否合適，也就變成了估計潛在變數之間相應的回歸係數（路徑係數）的值，而度量模型便是估計這些回歸係數的依據。
模型的評價
結構方程是模型的目標就是再生一個觀測變數的引申方差協方差矩陣Σ，使之與樣本方差協方差矩陣S儘可能地接近，同時評價模型對數據的擬合程度。如果引申的方差協方差矩陣Σ與樣本方差協方差矩陣S之間的差別非常小，也就是殘差矩陣各個元素接近於0，就可以認為模型擬合了數據。
關於模型的總體擬合程度有許多測量指標和標準，對模型的評價，涉及到模型對數據的總的擬合程度，AMOS軟體提供了多種判定擬合優度的量。用戶可以在模型上面直接給出擬合統計量，顯示統計量結果。
1.卡方統計量（X2）
在觀測變數服從多元常態分配且模型設定正確的話，如果分析方差協方差矩陣，則乘積服從卡方分布（或漸進服從卡方平方分布）。這裡需注意，它的檢驗正好與傳統的統計研究相反，我們希望得到的不顯著的卡方值，大的值對應差的擬合，小的值對應於好的擬合。事實上，這裡的卡方檢驗是“擬合劣度（badness-of-fit）”檢驗，很小的卡方值說明模型擬合很好。但是，卡方檢驗統計量與樣本量的大小密切相關，當樣本量越大，卡方值也越大，拒絕一個模型的機率就會隨著樣本量的增加而增加，也就是說，最好把卡方檢驗看成是度量擬合優度的量，而不是把它當作檢驗統計量。為減小樣本量對擬合檢驗的影響，習慣上採用卡方值與自由度之比，如果比值小於2，則可以認為模型擬合較好。
2.擬合優度指數（GFI）
擬合優度指數（goodness-of-fitindex）GFI度量了觀測變數的方差協方差矩陣S在多大程度上被模型引申的方差協方差矩陣所預測，如果Σ=S，GFI=1，意味著模型完美擬合。
3.修正的擬合優度指數（AGFI）
修正的擬合優度指數（adjustedgoodness-of-fitindex）AGFI利用模型中參數估計的總數與模型估計的獨立參數—自由度來修正，估計的參數相對於數據點越小，AGFI越接近GFI。
以上兩個指數都在0和1之間，較大的數對應於較好的擬合，一般大於0.9時，則認為模型擬合觀測數據。與X2不同的是，GFI和AGFI不是樣本容量的函式，因為它們並不是統計量，只是測量了樣本方差中估計方差所占的加權比例，因此不能用來對模型的擬合優度進行統計檢驗。
4.平方平均殘差的平方根（RMR）
平方平均殘差的平方根（rootmeansquareresidual）RMR度量了擬合殘差的一種平均值，說明樣本方差和協方差在假定模型正確的情況下的估計值的差異，RMR越小，說明擬合較好，如果RMR等於0，表明模型完美擬合。
5.本特勒-波內特規範指數（NFI）
本特勒-波內特規範指數（Bentler-Bonettnormedfixindex）是從設定模型的擬合（或是擬合函式，或用卡方值）與獨立模型（independencemodel）的擬合之間的比較。獨立模型是指假設所有變數之間沒有相關關係，也就是說，模型中所有的路徑係數和外生變數之間都固定為0，只估計方差。用來比較設定模型與獨立模型在擬合上的改善程度。
6.近似誤差的平方根（RMSEA）
近似誤差的平方根（rootmeansquareerrorofapproximation）。習慣上，RMSEA取值小於0.05，表明相對於自由度模型擬合了數據；另外，建議在90%的置信度下，如果RMSEA取值小於0.08，則可認為近似誤差是合理的，或者說在置信水平0.01下不能拒絕這一假設。RMSEA評價指標近年來越來越受到重視。
7.信息標準指數（informationcriteriaindex）
信息標準測量是為了作不同模型的比較，信息標準測量的值越小說明含獨立估計參數越少的模型擬合越好，也就是說簡約模型（parsimoniousmodel）越好。一般在設定的理論模型中，使用同一數據，按照理論減少模型中某個或某幾個自由參數，比較某種信息標準指數的差異，選擇指數最小的模型，也就是簡約模型。
需要強調的是，雖然這裡給出了許多評價模型擬合指數，但是沒有唯一的模型擬合標準指數是正確的。所以，在模型擬合過程中，要儘量納入各種指標，並儘可能地了解各種指數的內在含義，這可能完全需要研究者來判斷。
實際套用中，研究者還需要對度量模型和結構模型的可靠性和有效性進行必要的檢驗，一般可根據經典的檢驗理論，採用復相關係數和總決定係數說明單個觀測變數或全部觀測變數作為潛在變數的度量指標的可靠程度，以及單個或全部外生潛在變數對內生潛在變數的方差效應。
此外，模型及擬合的標準並不完全是統計問題，即使一個模型擬合了數據，也不意味著這個模型是“正確的”或是“最好的”。因為可能存在著等價模型（equivalentmodels），競爭模型（competingmodels）。如果簡單模型的擬合與複雜模型的擬合一樣好，就應該接受簡單模型，因為，我們的目標就是建立簡約模型，也就是說模型中的參數越少越好。因此，結構方程式模型的模型策略簡單就是美，最重要的是所有估計參數應該有實際意義，能夠得到合理的解釋，研究者始終應該將結構方程式模型建立在有說服力的理論假設上。
結構方程模型的優點
1.同時處理多個因變數
結構方程分析可同時考慮並處理多個因變數。在回歸分析或路徑分析中，就算統計結果的圖表中展示多個因變數，其實在計算回歸係數或路徑係數時，仍是對每個因變數逐一計算。所以圖表看似對多個因變數同時考慮，但在計算對某一個因變數的影響或關係時，都忽略了其他因變數的存在及其影響。
態度、行為等變數，往往含有誤差，也不能簡單地用單一指標測量。結構方程分析容許自變數和因變數均含測量誤差。變數也可用多個指標測量。用傳統方法計算的潛變數間相關係數，與用結構議程分析計算的潛變數間相關係數，可能相差很大。
3.同時估計因子結構和因子關係
假設要了解潛變數之間的相關，每個潛變數者用我個指標或題目測量，一個常用的做法 是對每個潛變數先用因子分析計算潛變數（即因子）與題目的關係（即因子負荷），進而得到因子得分，作為潛變數的觀測值，然後再計算因子得分，作為潛變數之間的相關係數。這是兩個獨立的步驟。在結構方程中，這兩步同時進行，即因子與題目之間的關係和因子與因子之間的關係同時考慮。
4.容許更大彈性的測量模型
傳統上，我們只容許每一題目（指標）從屬於單一因子，但結構方程分析容許更加複雜的模型。例如，我們用英語書寫的數學試題，去測量學生的數學能力，則測驗得分（指標）既從屬於數學因子，也從屬於英語因子（因為得分也反映英語能力）。傳統因子分析難以處理一個指標從屬多個因子或者考慮高階因子等有比較複雜的從屬關係的模型。
5.估計整個模型的擬合程度
在傳統路徑分析中，我們只估計每一路徑（變數間關係）的強弱。在結構方程分析中，除了上述參數的估計外，我們還可以計算不同模型對同一個樣本數據的整體擬合程度，從而判斷哪一個模型更接近數據所呈現的關係。
