基本介紹
- 中文名:納皮爾公式
- 外文名:Napier formulas
- 所屬學科:數學
- 所屬問題:球面三角
- 簡介:球面三角的基本公式之一
- 提出者:納皮爾(J.Napier)
- 套用:用於解球面斜三角形
基本介紹




納皮爾公式的證明









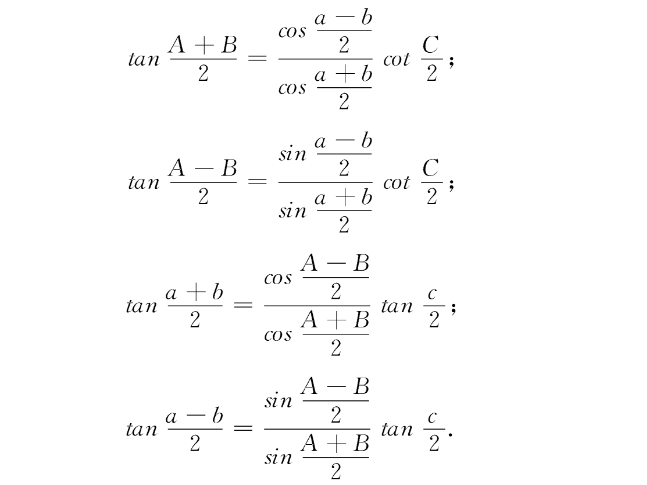













納皮爾公式(Napier formulas)是球面三角的基本公式之一,即球面三角形中兩角(邊)和、差之半的正切公式,是納皮爾(J.Napier)模仿平面三角中的正切定理推出的四個公式,用於解球面斜三角形。基本介紹在球面三...
納皮爾(Napier,1550~1617)是蘇格蘭梅爾契斯頓堡的貴族。他對數學有濃厚的興趣。他從幾何的研究入手,特別是受到三角公式 的啟發,認為乘除法運算可以用加、減法來代替。他通過20多年的潛心鑽研,終於給出了對數的幾何定義:設線段TS和射線BI為給定的。點P從T出發,沿TS作變速運動,其速度與它和S的距離成比例地...
4.納皮爾公式 1614年,蘇格蘭數學家納皮爾發明了對數的概念,它讓數學變得簡單快速,當然這不是他的唯一貢獻,他還是小數點的提倡者,直到後來才被人們接受。他還發明了一種計數公式:Napier’s Bones。它能夠幫人們演示加法中運用乘法,還有減法中的運用除法。他的發明中最為熟悉的是平方根和立方根,我們至今都在...
他重新建立了用於解球面直角三角形的10個公式的巧妙記法——圓的部分法則(“納皮爾圓部法則”)和解球面非直角三角形的兩個公式——“納皮爾比擬式”,以及做乘除法用的“納皮爾算籌”。此外,他還發明了納皮爾尺,這種尺子可以機械地進行數的乘除運算和求數的平方根。定義 若一個數x(x>0)經過一個對數函式...
對數也出現在許多科學公式中,例如Tsiolkovsky火箭方程,Fenske方程或能斯特方程。歷史 16、17世紀之交,隨著天文、航海、工程、貿易以及軍事的發展,改進數字計算方法成了當務之急。約翰·納皮爾(J. Napier,1550~1617)正是在研究天文學的過程中,為了簡化其中的計算而發明了對數.對數的發明是數學史上的重大事件,...
他重新建立了用於解球面直角三角形的10個公式的巧妙記法——圓的部分法則("納皮爾圓部法則")和解球面非直角三角形的兩個公式——"納皮爾比擬式",以及做乘除法用的"納皮爾算籌"。此外,他還發明了納皮爾尺,這種尺子可以機械地進行數的乘除運算和求數的平方根 在納皮爾所處的年代,哥白尼的“太陽中心說”剛剛...
這五個數組成了我們需要的納皮爾多邊形(納皮爾圓周),從這兒,可以得到每個角度的餘弦值等於:相鄰兩角度的餘切的乘積相對兩角度的正弦的乘積可以參考半正矢(Haversine formula),能在球面三角上解析弧長與角度,為航海學提供了穩定的模式。球面三角形 球面上過球心的平面與球面的交線叫球面上的大圓弧,球面三角形是...
納皮爾對數值計算頗有研究。他所製造的“納皮爾算籌”,化簡了乘除法運算,其原理就是用加減來代替乘除法。 他發明對數的動機是為尋求球面三角計算的簡便方法,他依據一種非常獨等的與質點運動有關的構想構造出所謂對數方法,其核心思想表現為算術數列與幾何數列之間的聯繫。在他的1619年發表《奇妙的對數表的描述》中...
納皮爾法則 為了便於記憶這十個直角三角形公式,聶比爾提出了一條很有用的定則。除掉直角C,用(90°-a)和(90°-b)分別代替夾直角的兩個邊a和b,然後把所得的五個元素依序排成一個圓(如圖9所示);這樣,每個元素有兩個相鄰元素和兩個相對元素。聶比爾定則為:每個元素的餘弦等於兩相鄰元素的餘切的...
奇妙的對數表的描述(Mirifici I_ogarithmorumcanonis descriptio, "”" ) 17世紀初西方數學著作.蘇格蘭數學家納皮爾(Napier , J.)著。奇妙的對數表的描述(Mirifici I_ogarithmorumcanonis descriptio, "”" ) 17世紀初西方數學著作.蘇格蘭數學家納皮爾(Napier , J.)著,1614年出版於愛丁堡.納皮爾是對數的...
