基本介紹
- 中文名:簡單高次不等式
- 所屬:初等數學重要內容之一
- 類型:通常為一元高次不等式
- 解法:為不等式組法、列表法等
列表法,分組法,
列表法
解題步驟是:
①將不等式化為(x-x1)(x-x2)…(x-xn)>0(<0)形式(各項x的符號化“+”),令(x-x1)(x-x2)…(x-xn)=0,求出各根,不妨稱之為分界點,一個分界點把(實數)數軸分成兩部分,n個分界點把數軸分成n+1部分……;
②按各根把實數分成的n+1部分,由小到大橫向排列,相應各因式縱向排列(由對應較小根的因式開始依次自上而下排列);
③計算各區間內各因式的符號,下面是乘積的符號;
④看下面積的符號寫出不等式的解集.
例題解不等式:(x-1)(x+2)(x-3)>0;
解:①檢查各因式中x的符號均正;
②求得相應方程的根為:-2,1,3;
③列表如下:
x<-2 | -2<x<1 | 1<x<3 | x>3 | |
x+2 | - | + | + | + |
x-1 | - | - | + | + |
x-3 | - | - | - | + |
各因式積 | - | + | - | + |
④由上表可知,原不等式的解集為:{x|-2<x<1或x>3}.
根軸法
①將不等式化為(x-x1)(x-x2)…(x-xn)>0(<0)形式,並將各因式x的係數化“+”;(為了統一方便)
②求根,並在數軸上表示出來;
③由右上方穿線,經過數軸上表示各根的點(為什麼?原因為:當x=+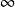 時不等式左側恆為正。);
時不等式左側恆為正。);
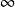
④若不等式(x的係數化“+”後)是“>0”,則找“線”在x軸上方的區間;若不等式是“<0”,則找“線”在x軸下方的區間.
注意:奇穿偶不穿
例題解不等式:(x-2)(x-3)(x+1)<0.
解:①檢查各因式中x的符號均正;
②求得相應方程的根為:-1,2,3(注意:2是二重根,3是三重根);
③在數軸上表示各根並穿線,每個根穿一次(自右上方開始),如下圖: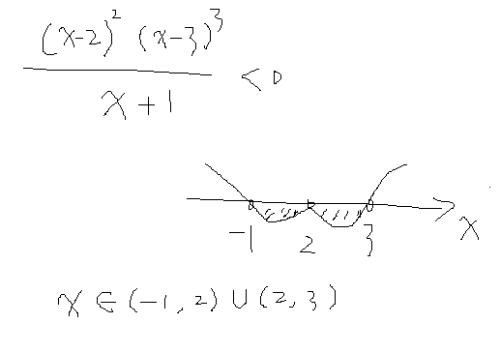
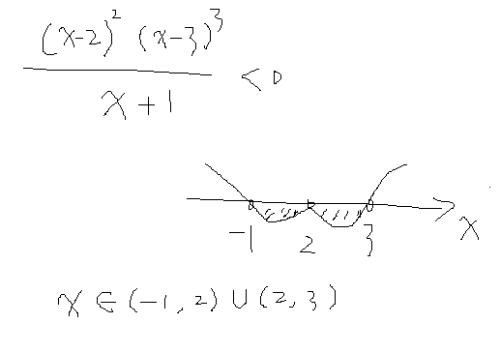
④∴原不等式的解集為:{x|-1<x<2或2<x<3}.
說明:∵3是三重根,∴在C處穿三次,2是二重根,∴在B處穿兩次,結果相當於沒穿.由此看出,當左側f(x)有相同因式(x-x1)時,n為奇數時,曲線在x1點處穿過數軸;n為偶數時,曲線在x1點處不穿過數軸,不妨歸納為“奇穿偶不穿”.
分組法
此種方法的本質是分類討論,強化了“或”與“且”,進一步滲透了“交”與“並”的思想方法
例題解不等式 x(3x2+2x-8)(1+x-2 x)≤0
解: 原不等式同解於 x(3x-4)(x+2)(2x+1)(x-1)≥0
先解不等式 x(3x-4)(x+2)(2x+1)(x-1)≥0 (*)同解於
x(x-4/3)(x+2)(x+1/2)(x-1)>0
由於 x-4/3< x-1<x< x+1/2< x+2
(1) x-4/3>0即x>4/3;
(2), x-1<0,x>0即0<x<1;
(3) x+2>0,x+1/2<0,即-2<x<-1/2。
所以,(*)的解是-2<x<-1/2或0<x<1或x>4/3.那么,原不等式的解是-2≤x≤-1/2或0≤x≤1或x≥4/3。