基本介紹
- 中文名:簡單幾何平均數
- 學科:數學
概念
計算公式
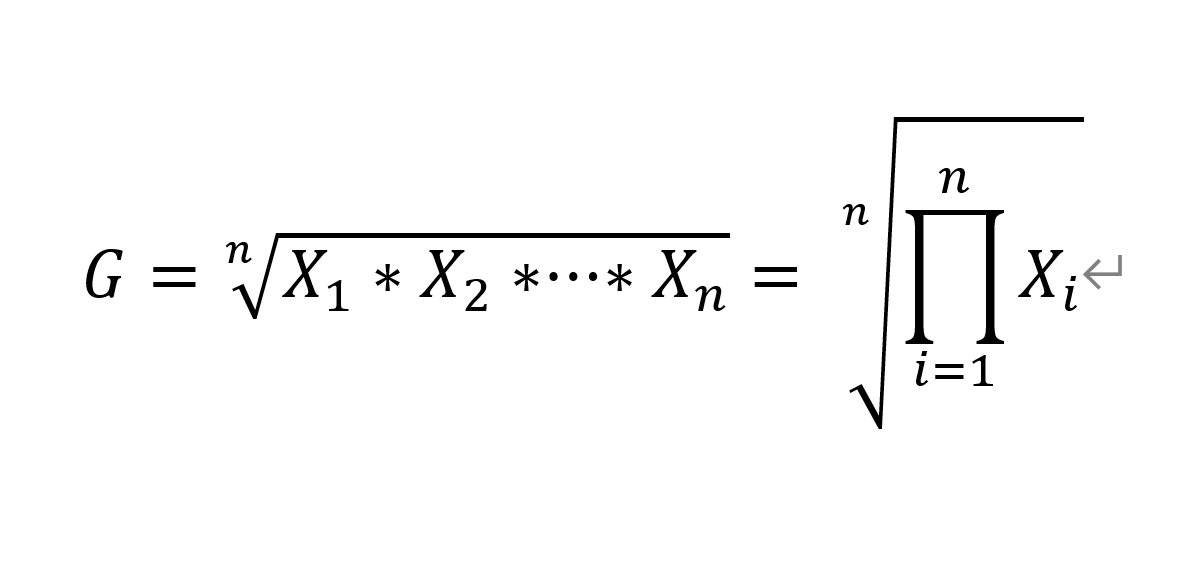
舉例分析


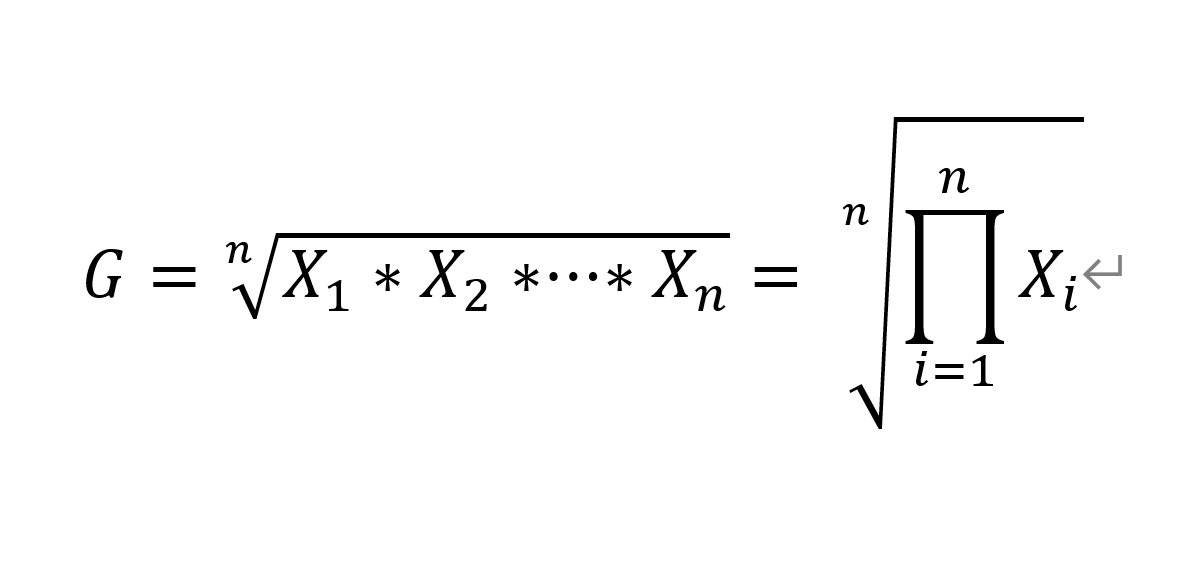

根據統計資料的不同,幾何平均數也有簡單幾何平均數和加權幾何平均數之分。簡單幾何平均數是n個變數值連乘積的n次方根。概念根據統計資料的不同,幾何平均數也有簡單幾何平均數和加權幾何平均數之分。簡單幾何平均數是n個變數值連乘積...
幾何平均數是n個變數值連乘積的n次方根。幾何平均數多用於計算平均比率和平均速度。如:平均利率、平均發展速度、平均合格率等。計算種類 1、簡單幾何平均法 2、加權幾何平均法 相關特點 1、幾何平均數受極端值的影響較算術平均數小。2、如果變數值有負值,計算出的幾何平均數就會成為負數或虛數。3、它僅適用於...
算術平均數是指在一組數據中所有數據之和再除以數據的個數。它是反映數據集中趨勢的一項指標。把n個數的總和除以n,所得的商叫做這n個數的算術平均數。公式:幾何平均數 geometric mean n個觀察值連乘積的n次方根就是幾何平均數。根據資料的條件不同,幾何平均數分為加權和不加權之分。公式:調和平均數 harmonic...
採用簡單幾何平均法計算的價格指數。在僅有商品價格資料,而無商品購銷數量或購銷金額的情況下,可用這種方法。計算價格指數時,首先計算各種商品價格在不同時期的比,再計算這些比的幾何平均數,以表明價格運動的趨勢及其幅度。計算公式為:簡單幾何平均價格 指數" src="" data-original="" align="absMiddle" title=...
簡單時間序列平滑法是指用簡單平均數進行預測的一類預測方法。當給定一組數據或觀測值後,這些數值的平均數的種類很多,常見的有算術平均數、幾何平均數、調和平均數、加權算術平均數、移動平均數與指數平滑平均數等。這些平均數各有各的計算方法,各有各的特點與用途,在使用平均法進行預測時,首先要判斷使用哪一種...
簡單幾何平均數的計算:加權幾何平均數的計算:位置平均數 位置平均數就是根據總體中處於特殊位置上的個別單位或部分單位的標誌值來確定的代表值,它對於整個總體來說,具有非常直觀的代表性,因此,常用來反映分布的集中趨勢。常用的有眾數、中位數。眾數——是總體中出現次數最多的變數值,在實際工作中有時有它的...
平均數指數 計算總指數的又一形式。它是個體指數的平均數(加權或不加權)。常用的有加權算術平均數指數、加權調和平均數指數和簡單幾何平均數指數。①加權算術平均數指數。以產品產量指數為例,其算式為:式中 為產量個體指數;W為權數。在有全面資料時,加權算術平均數指數實即綜合指數公式的變形 其權數要求為全面...
幾何平均數適用於計算現象的平均比率或平均速度。簡單幾何平均數適用於總體資料未經分組整理尚為原始資料的情況;加權幾何平均數適用於總體資料經過分組整理形成變數數列的情況。位置平均數:中位數、眾數。中位數是指將總體各單位標誌值按大小順序排列後,指處於數列中間位置的標誌值。不受極端數值的影響,在總體標誌值...
5.6.1簡單幾何平均數 5.6.2加權幾何平均數 5.7幾種平均數的關係 5.7.1算術平均數、眾數和中位數關係 5.7.2算術平均數和幾何平均數、調和平均數的關係 5.8計算和套用平均指標的原則 5.8.1總體各單位必須是同質的 5.8.2用組平均數來補充說明總平均數 5.8.3平均指標分析與變異指標分析相結合 思考與練習 第6章變...
6.3.2 加權調和平均數 6.3.3 相對指標和平均指標平均數的計算 6.4 幾何平均數 6.4.1 簡單幾何平均數 6.4.2 加權幾何平均數 6.5 眾數和中位數 6.5.1 眾數 6.5.2 中位數 6.6 各種平均數之間的相互關係 6.6.1 算術平均數、幾何平均數和調和平均數三者之間的關係 6.6.2 算術平均數與眾數、...
三、加權算術平均數 第三節調和平均數 一、調和平均數的概念和計算 二、調和平均數的套用 第四節幾何平均數 一、簡單幾何平均數 二、加權幾何平均數 第五節眾數和中位數 一、眾數 二、中位數 第六節標誌變異指標 一、標誌變異指標的概念和作用 二、標誌變異指標的種類和計算 習題四 第五章時間數列 第一節...
第四節 簡單的線性規劃 (7.4簡單的線性規劃;7.5研究性課題與實習作業)(62)第五節 圓的方程 (7.7圓的方程)(65)第八章 圓錐曲線方程(75)第一節 橢圓的標準方程與簡單幾何性質 (8.1橢圓及其標準方程;8.2橢圓的簡單幾何性質)(75)第二節 橢圓與直線的位置關係*(81)第三節 雙曲線的標準方程...
然後相加,最後計算出經濟效益指標的綜合評價指數。步驟 用各項指標實際值分別除以各項指標的評價標準值,得出各項指標的評價值 對於各項指標評價指數進行加權算術平均,得出綜合評價值 優點 方法簡單 經濟含義清晰 容易理解 缺點 指標要注意使用同向指標,如不同向,必須做好同向處理 ...
2.在比較簡單成對差異( simple pairwise differences)時,圖基法最具效力,給出更窄的置信區間,雖然它對於廣義比對( general contrasts) 也可適用。3.與此相比,對於涉及廣義比對的比較,謝弗法更具效力,給出更窄的置信區間。4.如果F檢驗顯著,那么謝弗法將從所有可能的比對(contrasts)中至少檢測出一對比對是...
下面用一個簡單的例子來說明方差分析的基本思想:如某克山病區測得11例克山病患者和13名健康人的血磷值(mmol/L)如下:患者:0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11 健康人:0.54 0.64 0.64 0.75 0.76 0.81 1.16 1.20 1.34 1.35 1.48 1.56 1.87 問該此...
泊松過程是萊維過程(Lévy process)中最有名的過程之一。時間齊次的泊松過程也是時間齊次的連續時間Markov過程的例子。一個時間齊次、一維的泊松過程是一個純出生過程,是一個出生-死亡過程的最簡單例子。泊松簡介 泊松,法國數學家,1781年6月21日生於法國盧瓦 雷省的皮蒂維耶,1840年4月25日卒於法國索鎮。1798年...
下面用一個簡單的例子來說明雙因素方差分析的基本思想:如某克山病區測得11例克山病患者和13名健康人的血磷值(mmol/L)如下:問該地克山病患者與健康人的血磷值是否不同?患者:0.84 1.05 1.20 1.20 1.39 1.53 1.67 1.80 1.87 2.07 2.11 健康人:0.54 0.64 0.64 0.75 0.76 0.81 1.16...
