簡介
在幾何形狀中,簡單多邊形是由直線,非相交的線段或“邊”組成的扁平形狀,其成對連線以形成封閉路徑。 如果兩邊相交,那么多邊形並不簡單。 經常省略限定詞“簡單”,上述定義通常被理解為多邊形。
簡單多邊形還可定義為:
1.周界不自交的多邊形。 2.滿足條件:
1)頂點與頂點不重合。
2)頂點不在邊上。
3.邊與邊不相交的多邊形。
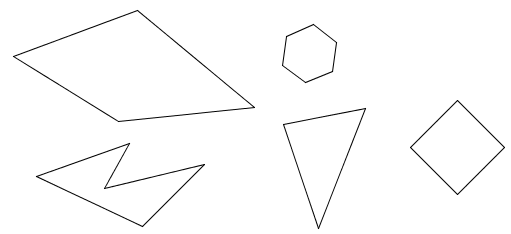
簡單多邊形分
凸多邊形和
凹多邊形兩種。
通常需要在拐角處相遇的兩個邊緣形成不直線(180°)的角度;否則,共線線段將被視為單側的部分。
數學家通常使用“多邊形”來表示由線段而不是封閉區域構成的形狀,然而有些可能使用“多邊形”來指由有限序列組成的封閉路徑限定的平面圖 的直線段(即通過閉合的多邊形鏈)。 根據使用的定義,該邊界可以不形成多邊形本身的一部分。
簡單的多邊形也被稱為約旦多邊形,因為約旦曲線定理可以用來證明這樣的多邊形將平面劃分成兩個區域,即它內部的區域和其外部的區域。 平面上的多邊形若且唯若在
拓撲上等同於一個圓時才是簡單的,它的內部在拓撲上等同於一個磁碟。
屬性
上面給出的定義確保了以下屬性:
1.多邊形包圍一個總是具有可測量區域的區域(稱為其內部)。
2.構成多邊形(稱為邊)的線段僅在其端點(稱為頂點)或更少的正式“角”處相遇。
3.兩個邊緣完全相交。
4.邊數總是等於頂點數。
弱簡單多邊形
如果非交叉線段的集合形成了與磁碟拓撲相當的平面區域的邊界,則該邊界稱為弱簡單多邊形。在右邊的圖像中,根據這個定義,ABCDEFGHJKLM是一個弱簡單的多邊形,藍色標記了它作為邊界的區域。這種類型的弱簡單多邊形可以在計算機圖形和CAD中出現,作為具有孔的多邊形區域的計算機表示:對於每個孔,創建“切割”以將其連線到外部邊界。參考上述圖像,ABCM是具有孔FGHJ的平面區域的外部邊界。切割ED將孔與外部連線,並在所得到的弱簡單多邊形表示中遍歷兩次。

在弱簡單多邊形的替代和更一般的定義中,它們是相同組合類型的簡單多邊形的序列的極限,在Fréchet距離下的收斂,這使得這樣的多邊形允許段接觸但不能交叉的概念形成。然而,這種類型的弱簡單多邊形不需要形成區域的邊界,因為其“內部”可以是空的。例如,參考上述圖像,根據該定義,多邊形鏈ABCBA是弱簡單的多邊形:它可以被視為多邊形ABCFGHA的“擠壓”的限制。
計算問題
在計算幾何中,幾個重要的計算任務涉及到一個簡單多邊形形式的輸入;在每個這些問題中,內部和外部之間的區別在問題定義中至關重要。
多邊形測試中的點涉及為簡單多邊形P和查詢點q確定q是否位於P內部。
計算多邊形面積的簡單公式是已知的;也就是多邊形內部的區域。
多邊形分區是一組不重疊的原始單位(例如正方形),其聯合等於多邊形。多邊形分區問題是在某種意義上找到最小的分區的問題,例如:具有最小單位數或具有最小總長度單位的分區。
多邊形分區的特殊情況是多邊形三角剖分:將簡單多邊形分成三角形。雖然凸多邊形易於
三角測量,但是對於一般簡單多邊形進行三角測量更為困難,因為我們必須避免增加跨多邊形的邊。然而,Bernard Chazelle在1991年表明,任何具有n個頂點的簡單多邊形可以在Θ(n)時間內進行三角測量,這是最佳的。也可以使用相同的算法來確定閉合多邊形鏈是否形成簡單多邊形。
多邊形上的
布爾運算:由多邊形區域定義的點集合的各種布爾運算。
簡單多邊形的凸包可以比其他類型的輸入的凸包更有效地計算,例如點集的凸包。












