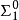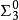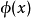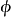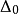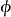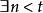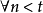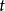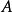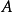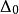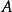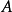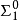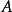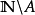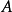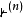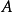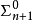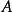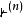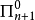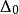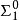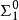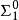基本介紹
- 中文名:算術階層
- 性質:可計算性理論中的概念
- 領域:計算機
定義,按公式定義,按可計算性定義,舉例,可計算性理論,
定義
按公式定義
定義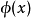 為
為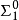 公式若且唯若
公式若且唯若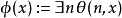 ,其中
,其中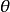 為
為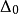 ;定義
;定義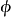 為
為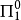 公式若且唯若
公式若且唯若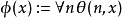 ,其中
,其中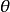 為
為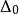 。
。
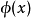
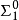
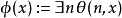
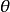
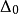
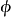
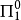
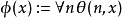
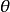
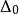
更進一步定義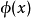 為
為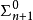 公式若且唯若
公式若且唯若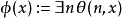 ,其中
,其中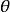 為
為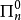 公式;定義
公式;定義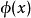 為
為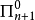 公式若且唯若
公式若且唯若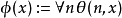 ,其中
,其中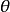 為
為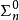 公式。
公式。
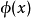
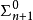
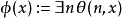
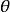
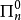
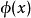
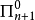
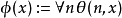
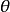
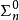
設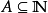 ;若存在
;若存在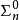 公式定義
公式定義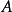 則稱
則稱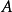 為
為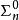 集合,若存在
集合,若存在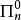 公式定義
公式定義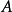 則稱
則稱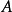 為
為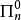 公式。(若有公式
公式。(若有公式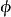 與集合
與集合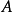 ,使
,使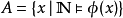 ,則稱
,則稱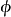 定義
定義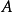 。)
。)
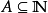
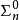
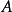
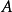
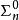
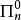
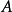
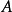
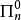
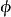
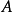
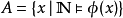
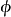
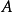
按可計算性定義
舉例
所有有限遞歸可枚舉集合的編號(記作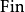 )是
)是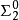 -完全集合(因此所有無限遞歸可枚舉集合的編號是
-完全集合(因此所有無限遞歸可枚舉集合的編號是 -完全集合)。
-完全集合)。
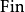
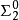

所有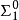 -完全集合作為遞歸可枚舉集合的編號是
-完全集合作為遞歸可枚舉集合的編號是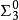 -完全集合。
-完全集合。