實軸和虛軸相等的雙曲線叫作等軸雙曲線(直角雙曲線)。
等軸雙曲線是指一種特殊的雙曲線，特點是漸近線互相垂直，半實軸長與半虛軸長相等，兩條漸近線y=±x互相垂直。
基本介紹
- 中文名：等軸雙曲線
- 外文名：Equilateral hyperbola
- 特徵：實軸和虛軸等長的雙曲線
- 又名：直角雙曲線
- 舉例：x2－y2＝a2、x2－y2＝﹣a2
- 所屬領域：數理科學
主要性質,相關命題,
主要性質
等軸雙曲線等軸雙曲線的主要性質有：
（1）半實軸長=半虛軸長（一般而言是a=b，但有些地區教材版本不同，不一定用的是a,b這兩個字母）；
（2）其標準方程為
，其中m≠0；
（3）離心率e=√2；
（4）漸近線：兩條漸近線 y=±x 互相垂直；
（5）等軸雙曲線上任意一點到中心的距離是它到兩個焦點的距離的比例中項；
（6）等軸雙曲線上任意一點P處的切線夾在兩條漸近線之間的線段，必被P所平分；
（7）等軸雙曲線上任意一點處的切線與兩條漸近線圍成三角形的面積恆為常數a^2；
（8）等軸雙曲線x^2-y^2=C繞其中心以逆時針方向旋轉45°後，可以得到XY=a^2/2，其中C≠0。
（9）反比例函式y=k/x的圖像一定是等軸雙曲線。
相關命題
1.設A是等軸雙曲線上一點，A處的法線分別交雙曲線的實軸m和虛軸n於B、C，那么，AB=AC。
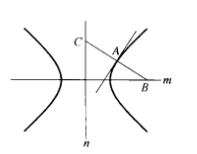圖12.設等軸雙曲線的中心為M，實、虛軸分別為m、n，過雙曲線上一點A作切線，且交n於B，設AM與m所成的角為α，AB與n所成的角為β，那么，α=β。
圖23.過等軸雙曲線的焦點F作兩條互相垂直的直線，且分別交雙曲線於A、B和C、D，那么，AB=CD。
圖34.以等軸雙曲線的弦AB為直徑作圓，且交雙曲線於C，過C作AB的垂線CS，那么，CS是雙曲線的切線。
圖45.設等軸雙曲線的實軸為AA’，弦BB’與AA’垂直，那么，AB⊥A’B’，A’B⊥AB’。
圖5