基本介紹
- 中文名:等腰三面角
- 外文名:isosceles trihedral angl
- 所屬學科:數學
- 所屬問題:立體幾何
- 簡介:有兩個面角相等的三面角
定義,相關定理及其證明,
定義
有兩個面角相等的三面角,稱為等腰三面角;三個面角皆相等的三面角,稱為等面三面角或正三面角。
如果將等腰三角形的兩腰換成等腰三面角的兩個相等的面角,將等腰三角形的兩底角換成等腰三面角的兩個相應的二面角,那么等腰三角形與等腰三面角有類似的性質。
相關定理及其證明
1. 等腰三面角中兩個相等的面角所對的二面角相等。
【例1】已知三面角的兩個面角相等,求證這兩個面角所對的兩個二面角相等。
證法一 設在三面角S-A' B'C'中,∠A'SB'=∠'B'SC' (圖1),在棱SB'上任取一點B,作BO⊥平面A'SC',垂足為O,作OA、OC分別與SA'、SC'垂直相交於A、C,連結AB、CB,則AB⊥SA',CB⊥SC',於是∠BAO和∠BCO分別是二面角B'-SA'-C'和二面角B'-SC'-A'的平面角。
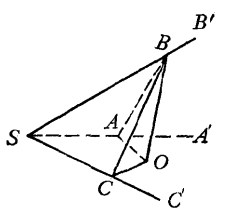 圖1
圖1在直角△SAB和直角△SCB中:
∵∠ASB=∠BSC,SB=SB,
∴直角△SAB≌直角△SCB,AB=CB,
又直角△ABO≌直角△CBO,
∴∠BAO=∠BCO,
∴二面角B'-SA'-C' =二面角B'-SC'-A'。
證法二在三面角S-ABC中(圖2),在平面SAC內作直線SD平分∠ASC,即∠ASD =∠DSC。由題設∠ASB=∠BSC,又∠BSD=∠BSD,因此三面角S-ABD和S-CBD的三個面角對應相等,但排列順序相反,所以這兩個三面角對稱,於是二面角B-SA-C和二面角B-SC-A相等。
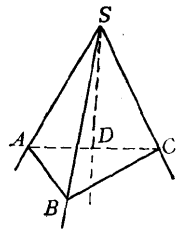 圖2
圖2本例的逆命題也是成立的。
2. 一個三面角能和它的對稱三面角互相重合的充要條件是它是等腰三面角。
3. 三面角中,如果兩個二面角不等,則二面角大的所對的面角較大。
4. 三面角中,如果兩個面角不等,則面角大的所對的二面角較大。
5. 兩個三面角中,如果兩個面角對應相等,而所夾的二面角不等,則第三個面角也不等,所夾二面角大的所對的面角也較大。
【例2】已知兩個三面角有兩個面角對應相等,而所夾的二面角不等。求證第三個面角也不等,較大的二面角所對的面角也較大。
證明在圖3的兩個三面角S-ABC和S'-A' B'C'中,∠ASB=∠A'S'B',∠BSC=∠B'S'C',二面角A'-S'B'-C'大於二面角A-SB-C,把這兩個三面角疊置起來使面ASB與面A'S'B'重合,那么面BSC必在二面角A'-S'B'-C'的內部。
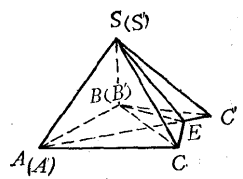 圖3
圖3在二面角C-SB-C'中,作平分面SBE交面ASC'於SE,
∵∠BSC=∠B'S'C',∠BSE=∠B'S'E',
二面角C-SB-E=二面角C'-S'B'-E,
∴三面角S-BEC和S'-B'EC'是相等的。
於是∠ESC=∠ES'C',
但在三面角S-ACE中:∠ASE+∠ESC>∠ASC,
用∠ES'C'代替∠ESC得:∠ASE+∠ES'C'>∠ASC,
即 ∠A'S'C'>∠ASC。
本例的逆命題也成立。
6. 兩個三面角中,如果兩個面角對應相等,而第三個面角不等,則它所對的二面角也不等,第三個面角大的所對的二面角也較大。