等積形

等積形(equiareal figure)是指具有等積關係的兩個圖形，面積相等的兩個圖形稱為等積形。例如，同底等高的兩個三角形就是等積形，三角形三頂點與其重心相連所成各三角形均為等積三角形，在三角形中只有重心有此性質。等底等高的平行四邊形是等積形，過平行四邊形對角線上一點，引各邊的平行線，所得四個平行四邊形中，不被對角線分割的兩個平行四邊形為等積形。

基本介紹

• 中文名：等積形
• 外文名：equiareal figure
• 簡介：面積相等的兩個圖形
• 所屬學科：數學（平面幾何）
• 舉例：同底等高的兩個三角形

基本介紹

等積形是指面積相等的疊疊棄平面圖形，兩個圖形等積，形狀不一定相同。例如，一個正方形長為6cm，它的和腳面積是36cm；一個梯形上底為4cm，下底為8cm，高為6cm，它的面積也是36cm，那么這個正方形與這個梯簽晚求膠形是等積形。又例如，同底等高的兩個三角形即為等積形，這一結論常用於直線圖形的等積變形。

常見等積形及證明

（1）在圖1中，直線l // BC， 為l上的點，則

圖1

（2）在永妹循圖2中，ABCD為梯形，O為對角線AC、BD的交點，如果DC// AB，則

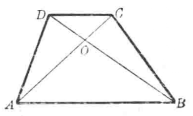
圖2

（3）在圖3中，P為平行四邊形ABCD對角線AC上一點，FF過P且平行於AB₂GH過P且平行於AD，則

S_{平行四邊形DEPH}=S_{平行四邊形PGBF}.

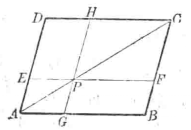
圖3

幾何圖形中等積形的證明，大都可以歸結為上述三個基本圖形、要證的等積形可通過添輔助線設法變形為同底等高的三角形，或者象圖船船棕蜜2、3那樣的梯形、平行四邊形，喇遷章就不難證明了。

相關定理

在等積形證明中，還有兩個基本定理須掌握：

(i)等底、等高的兩個三角形等積；

(ii)等底或等高的兩個三角形面積的比等於高的比或者底的比。

例題解析

【例1】與平行四邊形ABCD的對角線BD平行的直線PQ交BC於P，DC於Q，則（圖4）。

圖 4

證明 ∵PQ// BD，由基本圖形可得

又ABCD為平行四邊形，

∴ AD // BC，AB // DC，

及，

∴ .

【例2】在梯形ABCD中(圖5)，DC //AB，對斷協循角線AC與BD交於O，E為AB上任意一點，則

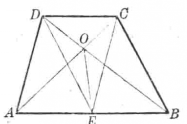
圖5

證明 ∵AB // DO，且E在AB上，

∴，

即

也就是

同理可證

所以