等機率假設(equal-probability hypothesis) 統計物理學的基本假設之一。對於由大量粒子組成的系統,粒子可能有多種分布,系統也就可以存在多種可能狀態。等機率假設是指對於系統的各種可能狀態,若沒有其他條件限定,就假定一切可能出現的狀態都是等機率的。
孤立系統與外界無任何聯繫,其能量保持不變。若用相空間點表示系統的狀態,則自然認為在等能面E與等能面E+△E間各點出現的機率應是一樣的,即分布密度函式ρ在此範圍內為常數,在此範圍外為零由此推出微正則系綜。進一步分析,得到與外界僅有能量交換和與外界有能量與物質交換的其他兩種平衡情況下,系統的分布函式和各種性質,進而建立起了統計物理學。
基本介紹
- 中文名:等機率假設
- 外文名:equal-probability hypothesis
- 提出者:玻爾茲曼
- 提出時間:1871年
- 一級學科:數學
- 二級學科:統計物理學
機率,等機率假設,在統計熱力學中的表達,
機率
在所有可能發生的事件(變數)中,某種事件(變數)發生可能性(或出現相對機會)的大小稱為該事件發生的機率。如果在N次(N很大)試驗中,某事件X出現了Ni次,則比值Ni/N就叫X事件出現的機率,用
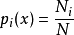
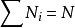
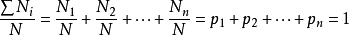
如果表示事件X的量 x 可以連續變化,我們就說 x 具有連續值譜。這時,x 出現在某一間隔 Δx 內的機率Δp(x) 應與這一間隔的位置 x 及大小Δx 有關。變數在 x 附近單位間隔內出現的機率稱為機率密度,用 f(x) 表示,於是便有Δp(x)=f(x)Δx。當Δx→0 時,Δp(x) 應寫成微分式
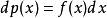
等機率假設
根據氣體動理論,當氣體處於平衡態時,雖然其巨觀態可以確定,但其微觀態卻仍不能確定(一切分子都處於永不停息的無規則運動中),而且也找不到任何理由來說明,某些微觀態要比另一些微觀態優越。基於這樣的事實,1871年,玻耳茲曼提出了著名的等機率假設:當系統處於平衡態時,其各個可能的微觀態出現的機率相等。對於氣體而言,等機率假設也可以這樣來表述:當氣體處於平衡態時,其分子向各個方向運動的機率相等。
等機率假設是平衡態統計理論的基礎,其正確性雖然不能直接由實驗來驗證,但由它所得到的許多推論都與客觀事實相符,因而便間接地證明了等機率假設是正確的。
在統計熱力學中的表達
所有能級分布微觀狀態數之和構成了系統的總微管狀態數,簡稱總微態數,用 Ω 表示
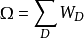
N、U、V確定的粒子系統,可能的能級分布方式D及其微管狀態數WD是確定的,系統的總微觀狀態數Ω也是確定的。也就是說,Ω是N、U、V的函式
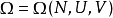
統計熱力學假設:對於N、U、V確定的粒子系統,每種微觀狀態出現的數學機率相等,均等於總微觀狀態數的倒數